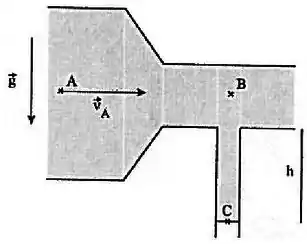
Considere o encanamento abaixo, por onde corre horizontalmente, em regime estacionário, um fluido não viscoso de densidade . A extremidade do cano vertical está aberta para a atmosfera e a coluna de líquido nele contida não cai.

Considere conhecidas a pressão , a seção reta e a velocidade no ponto , a altura do cano vertical, a gravidade e a pressão atmosférica .

1. Quais a velocidade e a pressão do fluido no ponto em função da seção reta no ponto ?
2. Discuta o sinal de a partir das expressões obtidas no item anterior.
3. Qual o valor de para que a coluna vertical de líquido não caia?

Aplicando equação de Bernoulli entre os pontos e :

Como , podemos eliminar o último termo de cada lado, pois são iguais:

A pressão e a velocidade foram dadas e podemos substituir pelo que encontramos:

Resolvendo item (b):

Pelo que acabamos de calcular:

Multiplicando por nos dois lados:

Logo:

Vamos analisar o sinal dessa expressão.

Para isso, basta analisarmos o termo entre colchetes, pois e são sempre positivos.

Sabemos, pela figura, que

Logo:

Ao quadrado:

Logo, o termo entre colchetes também é positivo.

Então é positivo!

Resolvendo item (c):

Se você achou estranho essa coluna de líquido “flutuando”, saiba que não foi só você que achou isso!

Mas o fato é que, se essa coluna está parada, vale a equação da hidrostática:

Olhando para a coluna de líquido, sabemos que, no fundo da coluna, a pressão é , a pressão no topo é e a profundidade é .

Logo:

Se isso não te convenceu, podemos fazer de outra maneira.

Se você entendeu o passo anterior, pode pular para o passo 7!

Como essa coluna está parada, então a soma das forças que atuam nela é zero!

Fazendo o diagrama de corpo livre na coluna de líquido:

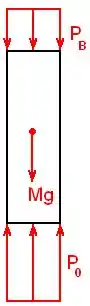
Note que, na parte superior da coluna, temos a pressão aplicada na área superior; e, na parte inferior, temos a pressão atmosférica atuando na área inferior.

Além disso, temos o peso da coluna de líquido.

Lembrando que pressão é força sobre área, podemos calcular as forças nas extremidades da coluna de líquido, multiplicando as pressões e pela área, que podemos chamar de :

Além disso, o peso é calculado como , sendo a massa total do líquido.

Pela figura, a força aponta para baixo e a força aponta para cima.

Somando as forças e igualando a zero:

Nós não sabemos o valor da área da coluna de líquido, nem a massa , mas sabendo sua altura .

Lembrando que volume é área vezes altura, podemos eliminar essa área da equação substituindo pelo produto da densidade pelo volume:

Mas , então:

Substituindo na equação:

Cancelando :

Uau! Que volta! Mas o resultado é o mesmo. Te convenci?

Agora é só substituir na equação que encontramos:

Mas o que queremos mesmo?

Ah, sim! A área . Então vamos isolar :

Multiplicando por os dois lados:

Pronto! Esse monstrinho é o que procurávamos!