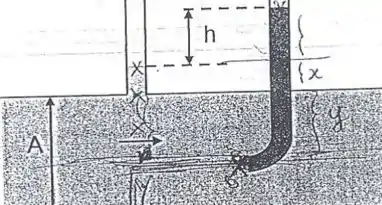
Quando um tubo retilíneo e outro com um cotovelo são acoplados a uma tubulação onde flui uma correnteza horizontal de água com velocidade , o nível da água no interior dos tubos começa a subir até que a pressão externa seja suficiente para estagnar o fluxo de água dentro dos tubos acoplados. Nesta situação, a diferença entre os níveis de água nos dois tubos verticais é , como ilustrado na figura. Considere um fluido ideal e
- Calcule a velocidade da correnteza.
- Considere que a área transversal, , é reduzida pela metade e a vazão mantida. Nesta situação, qual o novo valor de
Passo 1
a):
Bom, pra resolver essa questão. Nós vamos aplicar a equação de Bernoulli entre os pontos , o inicio do tubo em forma de cotovelo que está submerso, e , a superfície do fluido que está nesse mesmo tubo.
Beleza, então a equação de Bernoulli será:
A pressão de vai ser igual a coluna de fluido que existe acima dele mais a pressão atmosférica. Então:
Vamos considerar o nível zero de altura passando pelo ponto . Então:
A pressão do ponto vai ser iguala pressão atmosférica. E a altura vai ser a soma de todas as alturas:
Além disso, como o ponto está bem encima da superfície do líquido, a velocidade ali será zero;
Jogando todo mundo na equação de Bernoulli e chamando
Aplicando os valores do enunciado:
Passo 2
b):
A ultima expressão que a gente achou foi:
Como vemos, tem uma relação entre a velocidade e a altura. Entaõ:
Show! Agora, com a diminuição da área da seção transversal, qual será a nova velocidade do fluido? A gente precisa usar os conceitos de continuidade. A fórmula da continuidade é:
Então a redução da área pela metade fez a velocidade duplicar. Faz sentido né?
Então, a nova altura vai ser:
Resposta
a):
b):