Considere um corpo rígido constituído por 9 pequenas esferas de massa (que podem ser consideradas como partículas) ligadas por hastes de comprimento e massa desprezível conforme a figura.
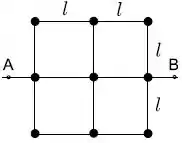
O momento de inércia desse corpo rígido em relação ao eixo é:
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
O momento de inércia de um sistema é a soma dos momentos de inércia de todos os elementos.
Então, mãos à obra, vamos calcular o momento de inércia de cada esfera e haste para depois somá-los.
Mas calma, ele diz que a massa das hastes é desprezível, logo, seus momentos de inércia serão nulos e sobram apenas as esferas.
Passo 2
O momento de inércia de uma partícula é dado por:
Onde é a distância ao eixo de rotação.
Passo 3
Começando com essas três esferas sobre o eixo:
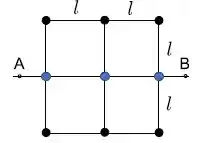
Como a distância delas ao eixo é zero, seu momento de inércia também é zero:
Já as outras 6 esferas, estão afastadas de uma distância do eixo , então:
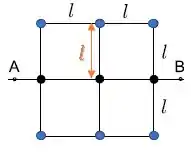
Passo 4
Somando os momentos de inércia de todos os elementos que calculamos, temos:
Ficamos com a letra (c).
Resposta
Letra (c)