UFRJ – Física 1 2020.2 – P2 – Questão 3
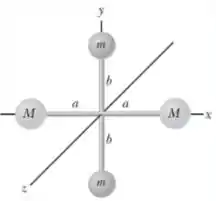
A figura abaixo mostra um sistema de quatro partículas unidas por barras de massa desprezível rígidas. Suponha que e seja maior do que . Considere momentos de inércia em relação aos eixos cartesianos indicados na figura , como se comparam os momentos de inércia?
Escolha uma:
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Essa questão é sobre momento de inércia de uma massa pontual e pra isso, precisamos lembrar como se calcula:
Onde é a distância da massa até o eixo de rotação, beleza?
Passo 2
Se esse sistema girar em torno do eixo as quatro massas vão contabilizar para o momento de inércia. A distância da massa até o eixo de rotação é e da massa aé o eixo é , assim o momento de inércia para o eixo é:
Como temos:
Certo?
Passo 3
E para o eixo ?
As massas que estão sobre esse eixo, não irão contribuir para o momento de inércia, pois elas estarão sobre o eixo de rotação (e, portanto, com ). A distância da massa até o eixo é . Então o momento de inércia para o eixo é:
Tranquilo?
Passo 4
E para o eixo ?
Levando em conta que o eixo está girando, agora são as partículas que não contabilizam para o cálculo do momento de inércia, uma vez que elas estão sobre o eixo de rotação.
A distância da massa até o eixo é . Assim o momento de inércia para o eixo é:
Passo 5
Agora vou contabilizar os resultados:
Como , podemos reescrever o momento de inércia de para fazermos a comparação:
Sabendo que , então fica claro que a ordem dos momentos de inércia é:
Ou melhor:
Analisando as alternativas, a correta é a (g).
Beleza?
Espero ter ajudado!