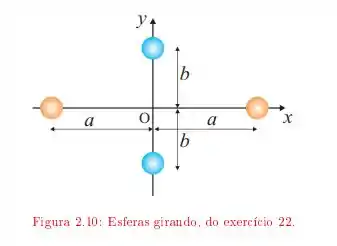
Quatro esferas pequenas de massa m estão presas às extremidades de uma estrutura de massa desprezível no plano xy.
b. Supondo que o sistema gire no plano xy ao redor de um eixo passando por O (eixo z), calcule o momento de inércia ao redor do eixo z e a energia rotacional ao redor desse eixo.
Passo 1
Eaew, belezinha?
Temos que determinar o momento de inércia do sistema ao redor do eixo z , sabemos que ele é dado por , sendo a massa de cada partícula do sistema e a sua distância do eixo de rotação. Também temos que determinar a energia cinética sabendo que ela é dada por . Vamos lá!
Passo 2
Temos que o momento de inércia será:
.
Então, temos que a energia cinética total será:
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
;