Tipler – Volume 1 – 6ª Ed. - Capítulo 9 – Seção 1 – Questão 41
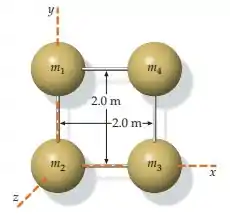
(Capítulo 9.1 – Exercício 41) Quatro partículas, uma em cada um dos cantos de um quadrado de de lado, estão ligadas por barras sem massa (figura 9-45). As massas das partículas são e . Determine o momento de inércia do sistema em relação ao eixo .
Passo 1
Oláaaa, queridão! Cê tá bem? Torcendo para que sim!
Então, o momento de inércia de uma partícula em relação ao um eixo é dado por
Onde é a massa da partícula e é a distância da partícula até o eixo em questão. No caso, o nosso eixo .
Maas, queremos o momento de inércia do sistema todo. Como faz?
Bem, o momento de inércia de um sistema de partículas é igual à soma do momento de inércia de cada uma das partículas, ou seja:
Então o que a gente vai fazer é calcular o momento de inércia de cada partícula em relação a , e depois somar tudo. Bora lá!
Passo 2
Então, para a partícula , o momento vai ser
Sendo que e a distância da partícula ao eixo é .
Para a partícula 2:
Temos . Mas repara que a partícula 2 está sobre o eixo . Então a distância dela até esse eixo é zero, .
Para a partícula 3:
Sendo que e a distância da partícula ao eixo é .
E para a acabar, temos a partícula :
Sendo que . E repara que vai ser a dimensão da diagonal desse quadrado de lado . A diagonal do quadrado vale sempre vezes o lado do quadrado. Então vamos ter
Passo 3
Agora é somar essa galera toda:
Substituindo os valores:
Obs: estamos diferentes do gabarito, mas estamos certinhos, tá?