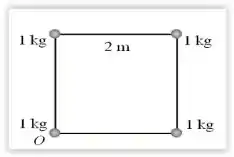
Quatro partículas de massas iguais a 1,0 kg estão ligadas por hastes rígidas e de massas desprezíveis formando um quadrado de lado 2,0m sobre um plano horizontal e sem atrito, conforme a figura. Qual é o momento de inércia do sistema em relação a um eixo perpendicular ao plano no qual se encontra o sistema e que passa pelo ponto O marcado na figura ?
(A) 4,0 kg
(B) 8,0 kg
(C) 10 kg.
(D) 16 kg
(E) 12 kg
Passo 1
Vamos aplicar a fórmula de momento de inércia para partículas:
Sabendo a o momento de inércia do sistema de partículas para o ponto O, será dado por:
Assim, vamos acha o I de cada partícula:
O momento de inércia da partícula que passa por O é nulo, pois r é nulo também.
O momento de inércia da partícula em cima da esquerda é:
O momento de inércia da partícula em cima da direita é:
O momento de inércia da partícula embaixo da direita é igual ao de cima da esquerda:
Somando todos:
- '' - ''Resposta
(D) 16 kg