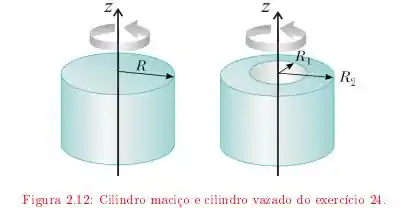
Um cilindro maciço de raio e massa tem . Utilizando este resultado, calcule o momento de inércia de um cilindro uniforme vazado de massa , de raio interno e externo , em relação ao eixo [veja a figura ].
Passo 1
Eaew, tudo certinho?
Temos que para um cilindro maciço de raio e massa o momento de inércia é dado por
No entanto, queremos utilizar este resultado para estimar o momentum de inércia no caso em que a massa é distribuída em um cilindro vazado de raio interno e raio externo , assim como podemos ver na figura
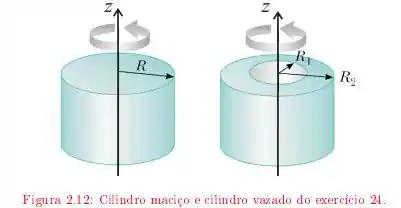
Para resolver este problema vamos usar o princípio de superposição! Ou seja, considerando que o buraco no interior é um cilindro de massa negativa, podemos calcular o momentum de inércia como
mas para isso vamos precisar avaliar a massa em cada “cilindro”! Saca só!
Passo 2
Se a massa for distribuída uniformemente ao longo de todo o sólido! Temos que a massa do exterior será dada por
Mas como encontramos esta densidade? Sabemos que a massa está distribuída sobre a casca cilíndrica de massa , o seu volume é dado por
em que é a altura do cilindro. Desta maneira, temos que a densidade será
Vamos usar isso para calcular a nossa massa!
Passo 3
Usando o volume do sólido completo como
temos que a massa será
Da mesma forma, podemos escrever a massa interna como
De forma que usando a fórmula
Podemos obter pelo princípio de superposição que
A questão foi isso! Te vejo na próxima! Tchau Tchau!