Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo do Momento de Inércia de Partículas

Ver Teoria
Exercício 213456789101112131415161718192021222324252627282930313233343536373839

Enunciado

As massas e coordenadas de quatro partículas são as seguintes:

50   g ,   x = 2,0   c m ,   y = 2,0   c m

25   g ,   x = 0 ,   y = 4,0   c m

25   g ,   x = - 3,0   c m ,   y = - 3,0   c m

30   g ,   x = - 2,0   c m ,   y = 4,0   c m

Quais são os momentos de inércia desse conjunto em relação ao eixos (a) x , (b) y e (c) z ? (d) Suponha que as respostas de (a) e (b) sejam A e B , respectivamente. Nesse caso, qual é a resposta de (c) em termos de A e B ?

Passo 1

Sabemos que:

I = ∑ I p a r t í c u l a = ∑ i 4 m i r i 2

Ou seja, vamos fazer para cada partícula:

  • Descobrir a distância até o eixo desejado
  • Elevar essa distância ao quadrado
  • Multiplicar pela massa da partícula

E depois iremos somar todos os resultados para obter o momento de inércia do conjunto em relação ao eixo.

Se desenharmos as posições dessas partículas, teremos:

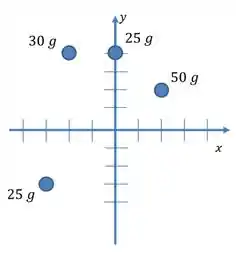
Vamos começar desenhando a distância de cada uma das partículas até o eixo x

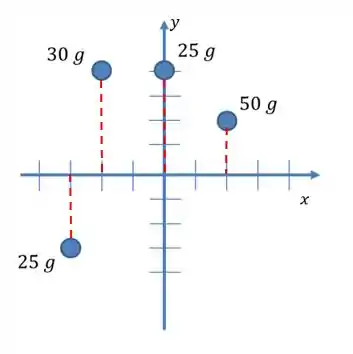
Assim o momento de inércia em relação a esse eixo será:

I x = 0,05   .   0,02 2 + 0,025   .   0,04 2 + 0,025   .   0,03 2 + 0,03   .   0,04 2

I x = 0,0001305   k g . m 2 → I x = 1,305   .   10 - 4   k g . m 2

Passo 2

Fazendo o mesmo pro eixo y :

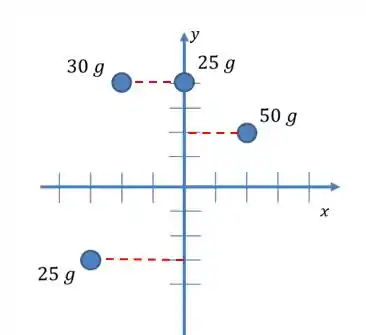
Repare que a massa de 25 g de cima está exatamente sobre o eixo y , o que significa que a sua distância até o eixo y é nula!

I y = 0,05   .   0,02 2 + 0,025   .   0 2 + 0,025   .   0,03 2 + 0,03   .   0,02 2

A segunda massa nessa equação aqui de cima tá exatamente sobre o eixo y , beleza? Isso faz com que a sua distância até o eixo y seja nula!

I y = 0,0000545   k g . m 2 → I y = 0,545   .   10 - 4   k g . m 2

Passo 3

Já para o eixo z , temos que usar o teorema de Pitágoras para achar a distância do ponto ao eixo:

d z = d x 2 + d y 2

Realizando o mesmo método:

I z = 0,05   .   ( 0,02 2 + 0,02 2 ) + 0,025   .   ( 0 2 + 0,04 2 ) + 0,03   .   0,02 2 + 0,04 2 +   0,025   .   0,03 2 + 0,03 2

I z = 0,000185 → I z = 1,85   .   10 - 4   k g . m 2

Outro jeito que a gente pode escrever é

d z 2 = d x 2 + d y 2

Ou seja

I z = ∑ m i d z i 2 = ∑ m i d x i 2 + d y i 2

E podemos dividir esse negócio em dois somatórios

I z = ∑ m i d x i 2 + ∑ m i d y i 2

Reconhece esses caras? Eles são I x e I y !!! :o

I z = I x + I y → I z = 1,305   .   10 - 4 + 0,545   .   10 - 4

I z = 1,85   .   10 - 4   k g . m 2

Resposta

  1. I x = 1,3   .   10 - 4   k g . m 2
  2. I y = 0,55   .   10 - 4   k g . m 2
  3. I z = 1,85   .   10 - 4   k g . m 2
  4. I z = I x + I y

Exercícios de Livros Relacionados

1. O centro de massa do haltere da FIGURA Q12.1 encontra-se no ponto a, b ou c? Explique.
Uma viga de 40k g e 5,0m de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na FIGURA P12.64. Um garoto de 20k g começa a caminhar ao longo da viga. Quão próximo ele pode ch
Integrando diretamente, calcule o momento de inércia de uma haste delgada de Massa M e comprimento L em torno de um eixo localizado a uma distância d de uma das extremidades. Confirme se sua resposta
Uma viga rígida com 3,0m de comprimento e massa de 100k g é apoiada em cada extremidade. Um estudante de 80k g encontra-se em pé a 2,0m do suporte 1. Que valor de força cada suporte exerce sobre a vig
Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y qu