USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 46
46. Duas barras idênticas, de mesma massa e comprimento, são usadas para desenhar um objeto com a forma da letra . Cada objeto pode girar em torno do eixo indicado pela linha tracejada na figura. Para os momentos de inércia a , relacionados com a rotação em torno ao eixo indicado, pode-se afirmar que:
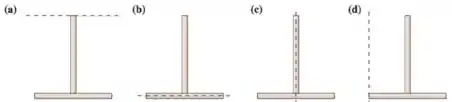
(a) .
(b) .
(c) .
(d) .
(e) .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos que ranquear os momentos de inércia dos exemplos dados na figura do exemplo.
Tem ideia de como fazer isso? 🤔
O momento de inércia obtido pelo teorema dos eixos paralelos como
Ou seja, quanto menor , menor o momento de inércia.
Considerando que cada barra possui massa e comprimento
Passo 2
Portanto, se analisarmos como a massa de cada caso está destruída em relação ao eixo de rotação, podemos perceber que é a maior de todas pois tem uma barra com centro de massa deslocado do eixo de rotação e outra barra a uma distância do eixo...
Agora podemos perceber que o momento do item é menor que o item pois tem uma haste deslocada a do eixo de rotação e outra barra perpendicular ao eixo de rotação, porém com centro de massa mais próximo do eixo de rotação.
O terceiro maior podemos perceber que é o item pois a barra da horizontal não interfere no momento de inercia e a barra da vertical está com o centro de massa deslocado a do eixo de rotação.
E finalmente o menor momento de inercia é obtido no item onde a barra da vertical não influencia no momento e a barra da horizontal tem o centro de massa no eixo de rotação, fazendo o caso com a melhor distribuição do centro de massa.
Portanto temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
(a) .