Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo do Momento de Inércia de Partículas

Ver Teoria
Exercício 361234567891011121314151617181920212223242526272829303132333435373839

Enunciado

Três massas, m 1 = m , m 2 = 2 m e m 3 = 3 m   estão afixadas em uma barra de massa desprezível que gira em torno do eixo O com velocidade angular ω , conforme a figura.

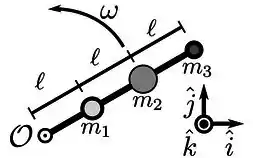
Qual o momento de inércia do conjunto de massas na figura em relação ao eixo?

  1. I = 10 m l 2
  2. I = 18 m l 2
  3. I = 26 m l 2
  4. I = 30 m l 2
  5. I = 36 m l 2
  6. I = 4 0 m l 2

Passo 1

Temos que o momento de inércia é dado por

I = ∑ m r 2

Como a massa da barra é desprezível vamos contar somente as contribuições das massas m 1 , m 2 e m 3 .

A massa m 1 está a uma distância l do centro de rotação, a massa m 2 está a uma distância 2 l e a massa m 3 está a uma distância 3 l , assim

I = m 1 l 2 + m 2 2 l 2 + m 3 3 l 2

I = m l 2 + 2 m × 4 l 2 + 3 m × 9 l 2 = m l 2 + 8 m l 2 + 27 m l 2

I = 36 m l 2

Resposta

(E)

Exercícios de Livros Relacionados

1. O centro de massa do haltere da FIGURA Q12.1 encontra-se no ponto a, b ou c? Explique.
Uma viga de 40k g e 5,0m de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na FIGURA P12.64. Um garoto de 20k g começa a caminhar ao longo da viga. Quão próximo ele pode ch
Integrando diretamente, calcule o momento de inércia de uma haste delgada de Massa M e comprimento L em torno de um eixo localizado a uma distância d de uma das extremidades. Confirme se sua resposta
Uma viga rígida com 3,0m de comprimento e massa de 100k g é apoiada em cada extremidade. Um estudante de 80k g encontra-se em pé a 2,0m do suporte 1. Que valor de força cada suporte exerce sobre a vig
Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y qu