Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo do Momento de Inércia de Partículas

Ver Teoria
Exercício 391234567891011121314151617181920212223242526272829303132333435363738

Enunciado

USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II, Questão 23

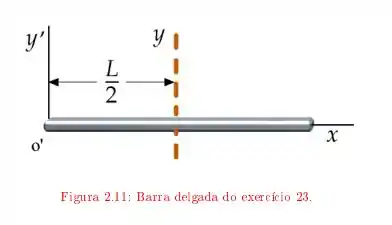
Uma barra na, com uma distribuição de massa uniforme, tem massa M e comprimento L. Calcule o seu momento de inércia em relação a um eixo (y) que passa pelo centro da barra e é perpendicular ao plano xz . Usando o teorema dos eixos paralelos, determine o momento de inércia em relação ao eixo y ′ , que passa por O′ e é paralelo ao eixo y.

Passo 1

Eaew, belezinha?

Temos que determinar o momento de inércia do sistema ao redor do eixo y’ utilizando o teorema dos eixos paralelos, sabemos que ele é dado por I y ' = I y + M d 2 , sendo d a distância entre os eixos, nesse caso, d = L 2 . Vamos lá!

Passo 2

Temos que o momento de inércia com relação ao centro da barra será:

I y = ∫ - L / 2 L / 2 x 2 d m .

Como a barra é homogênea, temos que

  d m d x = M L

d m = M L d x

Então, temos que

I y = ∫ - L / 2 L / 2 x 2 d m = M L ∫ - L / 2 L / 2 x 2 d x = M L ( x 3 3 ) | L / 2 - L / 2 = M L 2 12

Passo 3

Usando o teorema dos eixos paralelos, temos que

I y ' = I y + M d 2 = M L 2 12 + M L 2 4 = M L 2 3 .

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

I y ' = M L 2 3 .

Exercícios de Livros Relacionados

1. O centro de massa do haltere da FIGURA Q12.1 encontra-se no ponto a, b ou c? Explique.
Uma viga de 40k g e 5,0m de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na FIGURA P12.64. Um garoto de 20k g começa a caminhar ao longo da viga. Quão próximo ele pode ch
Integrando diretamente, calcule o momento de inércia de uma haste delgada de Massa M e comprimento L em torno de um eixo localizado a uma distância d de uma das extremidades. Confirme se sua resposta
Uma viga rígida com 3,0m de comprimento e massa de 100k g é apoiada em cada extremidade. Um estudante de 80k g encontra-se em pé a 2,0m do suporte 1. Que valor de força cada suporte exerce sobre a vig
Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y qu