A figura mostra dois sistemas A e B que diferem apenas na distância entre as pequenas esferas colocadas na haste fixa na polia. Os dois sistemas são abandonados a partir do repouso da mesma altura em relação ao solo. Os tempos para o bloco dos sistemas A e B chegar ao solo são respectivamente tA e tB. Qual é a afirmativa correta para a relação entre estes tempos?
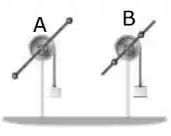
a) , porque a aceleração angular do sistema A é maior que do sistema B.
b) , porque a aceleração angular do sistema A é maior que do sistema B.
c) , porque os dois sistemas têm massas iguais.
d) , porque o torque da força peso do bloco pendurado é igual nos dois
sistemas.
e) , porque o momento de inércia do sistema A é maior que do sistema B.
Passo 1
Como a gente já viu na questão anterior, pra gente calcular o Momento de Inércia é assim:
Como a única coisa que difere esses sitemas são a distância, a gente sabe que o Momento de Inércia de A é maior que o de B, consequentemente o tempo de chegar ao solo vai ser maior! Tranquilo? :D
Resposta
e) , porque o momento de inércia do sistema A é maior que do sistema B.