Um sistema é composto por esferas de massas: , e , conforme a Figura. O sistema gira em torno do eixo com velocidade angular , no sentido Horário pra quem vê o sistema de cima. No que segue desconsidere a Massa das hastes e considere as esferas como partículas pontuais.
- Determinar a inércia rotacional do sistema em torno do eixo
- Calcule o momento angular (módulo, direção e sentido) do sistema.
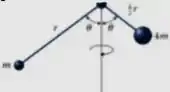
Passo 1
Bem, de acordo com a nossa teoria, podemos calcular a inércia rotacional de uma partícula girando em torno de um eixo pela fórmula:
Onde é a distância dessa massa ao eixo de rotação.
No nosso caso, o eixo passa em cima de uma das massas , logo ela não contribui para a inércia do sistema. Em contrapartida, as outras duas contribuem sim, e então a inércia rotacional do sistema vai ser a soma dessas contribuições:
Onde a massa é a massa e a massa 2 é a massa ...
e , por serem a distância até o eixo de rotação das massas...
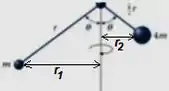
Por trigonometria, podemos falar que...
De modo que a inércia rotacional será...
Passo 2
POW! O módulo do momento angular pode ser dado por...
Então...
A direção e o sentido podem ser tirados da regra da mão direita: Se a haste gira no sentido horário, então fazendo os dedos (de menos o dedão) girar no sentido horário, o dedão vai ficar pra baixo, indicando que a direção é o sentido do eixo e o sentido para baixo:
Resposta
Letra A:
Letra B: