Considere um sistema de cinco objetos puntiformes dispostos em um plano de acordo com a figura a seguir. Cada um dos quatro objetos periféricos possui massa igual a , enquanto que o quinto, localizado na origem do sistema de coordenadas indicado na figura, tem massa . Eles são unidos por hastes rígidas e de massas desprezíveis.

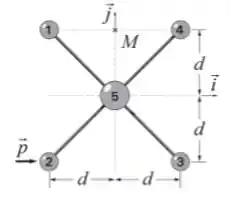
Calcule o momento de inércia do sistema em relação ao eixo passando pelos objetos e .

Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pela origem.

Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pelo ponto indicado na figura.

Temos agora o eixo passando perpendicularmente ao objeto 5. Neste caso, as distâncias dos objetos 1 ao 4 serão os comprimentos das hastes. Então os vetores posições serão agora:

Com o eixo passando pelo ponto , teremos as seguintes distâncias:

Para calcular as distâncias das partículas 2 e 3 ao eixo, podemos atentar para o triângulo azul abaixo:

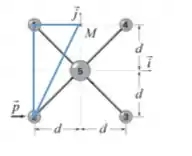
A distância (que é igual a ) é dada pela hipotenusa do triângulo! Logo, temos:

Continuando, teremos: