USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 45
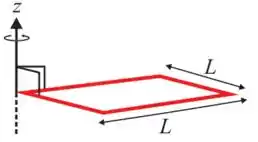
45. Um objeto quadrado de massa é formado por quatro varetas finas idênticas, todas de comprimento e massa , amarradas juntas. O objeto é fixado a uma barra, podendo girar em torno dela com velocidade angular , como mostrado na figura. O momento de inércia do objeto, em relação ao eixo de rotação (eixo z) na figura é:
(a) .
(b) .
(c) .
(d) .
(e) .
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉
Nesse problema queremos obter o momento de inercia do sistema composto por quatro hastes de comprimento que formam um quadrado e giram com o eixo de rotação em um vértice do quadrado.
Tem ideia de como fazer isso?
Para resolver esse problema, temos que aplicar o teorema dos eixos paralelos.
Esse teorema é calculado como
Tranquilo? Bora começar! 😁
Passo 2
O momento de inercia no eixo das extremidades das hastes é dado por
Agora vamos olhar para o centro do quadrado...
A diagonal do quadrado é dada por
Como o centro do quadrado fica na metade da sua diagonal, então
Substituindo em , temos
Pegou o esquema? Responde Aí! 😁
Resposta
(c)