USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 25c
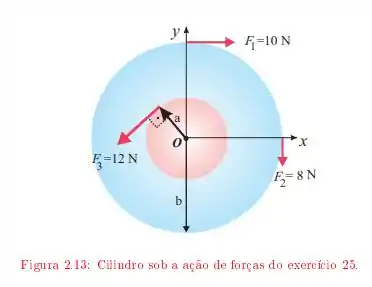
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .
Sabendo que a velocidade angular inicial do cilindro era , determine .
Passo 1
Oiie, tudo bem?
Temos um cilindro de massa , e sobre este cilindro são realizadas forças em diversas direções e posições no cilindro, como no esquema a seguir
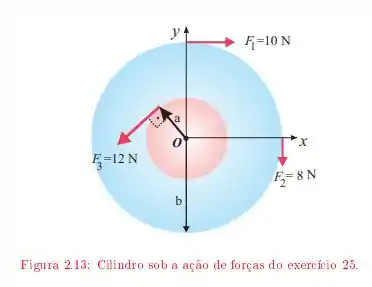
o cilindro vermelho tem raio dado por e o cilindro azul tem raio . Esta alternativa pede para que calculemos
Sabendo que a velocidade angular inicial do cilindro era , determine .
Nós obtivemos na questão anterior uma aceleração angular constante da forma
Como esta aceleração é constante, temos que a velocidade angular pode ser obtida como
Vamos aplicar esse resultado! Você pode demonstrar ele através de integração simples e
Mas o ponto do exercício não é esse! Bora lá!
Passo 2
Usando a velocidade inicial dada e a aceleração angular, temos que
ou ocultando as unidades, temos que
Essa alternativa foi isso! Te vejo na próxima! Até já!