Considere o circuito em corrente alternada mostrado em figura.
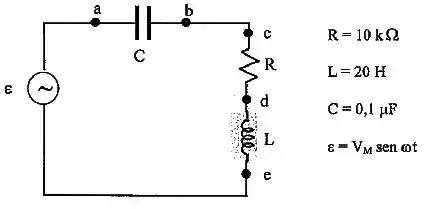
Sabendo que o valor máximo da tensão medida no capacitor (entre os pontos "a" e "b") é e que a frequência angular do gerador é :
Calcule o valor máximo da tensão entre os pontos “c” e “d” do circuito;
Calcule o valor máximo da tensão entre os pontos “d” e “e” do circuito;
Chamando , e , respectivamente, as tensões máximas no resistor, no capacitor e no indutor, desenhe (em escala) o diagrama dos fasores do circuito, indicando claramente , , e a corrente máxima .
Utilizando o diagrama, calcule a fase entre a tensão do gerador e a corrente que passa no circuito e o valor máximo da tensão do gerador, . Neste caso, o circuito possui comportamento indutivo ou capacitivo? Justifique a sua afirmação.
O circuito encontra-se em ressonância? Se sim, explique porque. Se não, calcule o valor do capacitor ou o indutor para que isso aconteça, mantida a frequência angular do gerador .
Passo 1
Calcule o valor máximo da tensão entre os pontos “c” e “d” do circuito;
A tensão entre os pontos “c” e “d” corresponde à tensão no resistor, dado por:
Como o problema nos deu o valor da resistência, precisamos descobrir a corrente máxima.
O problema nos disse que , e . Dessa forma:
Onde .
Substituindo os valores, teremos:
Finamente, a máxima tensão entre os pontos “c” e “d” será dada por:
Onde .
Passo 2
Calcule o valor máximo da tensão entre os pontos “d” e “e” do circuito;
A máxima tensão entre os pontos “d” e “e” do circuito corresponde à máxima tensão no indutor, dada por:
Onde e .
Passo 3
Chamando , e , respectivamente, as tensões máximas no resistor, no capacitor e no indutor, desenhe (em escala) o diagrama dos fasores do circuito, indicando claramente , , e a corrente máxima .
Para desenhar o diagrama de fasores precisamos relembrar algumas coisas:
- A tensão no resistor e a corrente estão em fase, ou seja, o ângulo de rotação do fasor é o mesmo de .
- A corrente está adiantada em relação à tensão no capacitor, ou seja, o ângulo de rotação do fasor é o mesmo da corrente menos .
- A corrente está atrasada em relação à tensão no indutor, ou seja, o ângulo de rotação no fasor é o mesmo da corrente mais .
Dessa forma, teremos o seguinte diagrama:
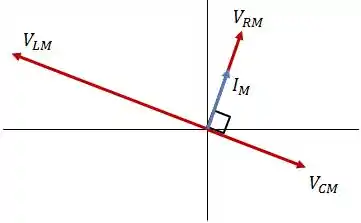
Lembrando que e .
Passo 4
Utilizando o diagrama, calcule a fase entre a tensão do gerador e a corrente que passa no circuito e o valor máximo da tensão do gerador, . Neste caso, o circuito possui comportamento indutivo ou capacitivo? Justifique a sua afirmação.
No diagrama de fasores, a tensão máxima no gerador e o ângulo de fase são indicados da seguinte forma:
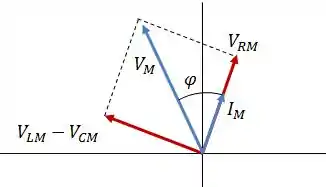
Dessa forma, utilizando o teorema de Pitágoras, o valor máximo da tensão no gerado será:
Passo 5
O ângulo de fase será dado por:
Passo 6
Um circuito possui comportamento indutivo se a reatância indutiva for maior que a reatância capacitiva. Da mesma forma, um circuito possui comportamento capacitivo se a reatância capacitiva for maior que a reatância indutiva.
Logo:
Finalmente:
Dessa forma, o circuito possui comportamento indutivo.
Passo 7
O circuito encontra-se em ressonância? Se sim, explique porque. Se não, calcule o valor do capacitor ou o indutor para que isso aconteça, mantida a frequência angular do gerador .
O circuito está em ressonância se , o que não é o caso aqui como vimos no Passo anterior.
Assim, vamos calcular o valor do capacitor (mantendo-se o indutor) e do indutor (mantendo-se o capacitor) para que isso aconteça.
A frequência de ressonância é dada por:
Dessa forma, mantendo-se o indutor, o capacitor será dado por:
Agora, mantendo-se o capacitor, o indutor será dado por:
Resposta
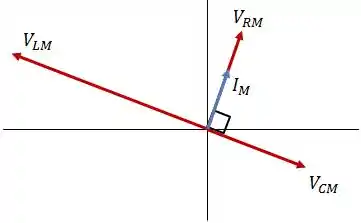
O circuito possui comportamento indutivo.