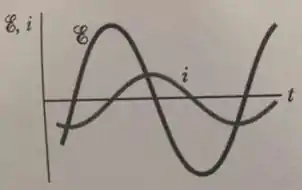
A figura mostra a corrente e a força eletromotriz de um circuito RLC em série. Para aumentar a potência transferida para o resistor, é preciso:
- Aumentar o valor de ;
- Aumentar o valor de ;
- Diminuir o valor de ;
- Aumentar o valor de ;
- Aumentar o valor da frequência da fonte;
Passo 1
O gráfico mostra que a fem alternada e a corrente estão defasadas entre si. Nesse caso, portanto, a frequência angular da fonte é diferente da frequência de ressonância para a qual a amplitude da corrente é máxima.
De maneira geral, a amplitude da corrente em um circuito RLC é dada por
em que é a amplitude da voltagem da fonte, que é fixa, e a é a impedância dada por
com e . Na ressonância, e , o que dá, para o valor máximo da corrente,
A potência média fornecida pela fonte para o resistor é dada por:
sendo que a fase tem a seguinte expressão:
que, na ressonância () é igual a e a potência média é máxima e dada por .
Agora, vamos analisar os itens considerando o circuito fora da ressonância, sempre considerando a potência média acima. Para isso, vamos precisar analisar tanto a impedância , quando a fase , já que ambas dependem de , , e .
Passo 2
Considerando a frequência angular da fonte fixa:
a) Aumentando o valor de , aumenta e a diminui e a fase também aumenta (porque aumenta), o que faz com que o tenha um valor menor. O resultado total neste caso será uma potência média menor.
b) Aumentando o valor de , aumenta e a diminui e a fase também aumenta (porque diminui), o que faz com que o tenha um valor menor. O resultado total neste caso também será uma potência média menor.
c) No entanto, se diminuímos o valor de , a impedância diminui e aumenta. No entanto, como a frequência de ressonância é
diminuir implica aumentar o valor de . Ao mesmo tempo, diminuir , faz com que a fase também diminua. Portanto, diminuir o valor de faz com que aumente e diminua e, consequentemente, a potência média aumente.
Este item, portanto, está CORRETO, mas vamos continuar analisando o restante. ;-)
d) Se somente aumentamos , a impedância aumenta e, consequentemente, diminui. Podemos descartar essa possibilidade, pois isso implicaria em menor.
e) Como a fonte está adiantada com relação à corrente, ou seja, , então aumentar a frequência da fonte, fará com que a amplitude da corrente diminua e a fase aumente, fazendo que tanto diminua quanto com que diminua. Por isso, aumentar implica em diminuir .
Resposta
Letra c.