Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fasores e Circuitos RLC

Ver Teoria
Exercício 711234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697072737475767778798081828384858687888990919293949596979899100

Enunciado

Circuito CA

No circuito R L C mostrado na figura abaio, a corrente é dada por i t = I sen ⁡ ω t - ϕ e a fonte de f e m é ε t = ε m sen ⁡ ω t . A reatância capacitiva 1 / ω C deste circuito é X C = 40 Ω .

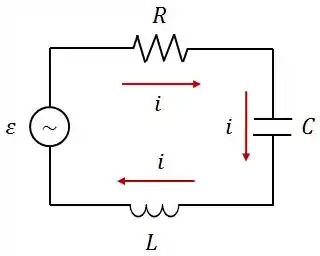
  1. Qual a impedância do circuito?
  2. Qual o valor da indutância?
  3. Qual é a constante de fase ϕ ?
  4. Qual a potência média dissipada no resistor?
  5. Para qual frequência da fonte a potência média dissipada em R será máxima? Especificar.

Dados: I = 2,0 A , ε m = 200 V , R = 80 Ω e ω = 200   r a d / s .

Passo 1

  1. Qual a impedância do circuito?

    2. A impedância do circuito pode ser calculada simplesmente por:

    Z = ε m I

    Z = 200 2 = 100   Ω

    Passo 2

  2. Qual o valor da indutância?

    3. Opa! Vamos lá!

    A impedância do circuito pode ser calculada também por:

    Z = R 2 + X L - X C 2

    Onde:

    X L = ω L

    Sendo que o problema já nos deu R , X C , ω e nós acabamos de calcular Z ... já viu que isso vai dar samba?

    Isolando o X L daquela equação, teremos:

    X L = X C + Z 2 - R 2

    L = X C + Z 2 - R 2 ω

    L = 40 + 100 2 - 80 2 200

    L = 40 + 60 200

    L = 0,5 H

    Passo 3

  3. Qual é a constante de fase ϕ ?

    4. O ângulo de fase é dado por:

    t g ϕ = X L - X C R

    Onde X L = ω L = 200 × 0,5 = 100   Ω .

    t g ϕ = 100 - 40 80 = 3 4

    ϕ = arctan ⁡ 3 4

    Passo 4

  4. Qual a potência média dissipada no resistor?

    5. A potência dissipada no resistor é dada por:

    P = I 2 R

    Mas como a corrente varia com o tempo, a potência média dissipada é dada por:

    P m = I r m s 2 R

    Onde I r m s é o valor quadrático médio da corrente, dado por:

    I r m s = I m á x 2

    Logo:

    P m = I 2 2 R

    P m = 2 2 2 × 80

    P m = 160 W

    Passo 5

  5. Para qual frequência da fonte a potência média dissipada em R será máxima? Especificar.

A potência média dissipada em R será máxima quando a frequência for igual à frequência de ressonância.

ω 0 = 1 L C

Onde C = 1 / ω X C .

ω 0 = 1 0,5 40 × 200 = 40 × 200 0,5

ω 0 = 126   r a d / s

Resposta

a.

Z = 100   Ω

b.

L = 0,5 H

c.

ϕ = arctan ⁡ 3 4

d.

P m = 160 W

e.

ω 0 = 126   r a d / s

Exercícios de Livros Relacionados

Na Fig. 31-37, um gerador trifásico G produz energia elétrica que é transmitida através de três fios. Os potenciais dos três fios (em relação a uma referência comum) são V 1 = As e nω t para o fio 1,
Que corrente contínua produz a mesma energia térmica, em um certo resistor, que uma corrente alternada com um valor máximo de 2,60A ?
A figura 31-35 mostra um gerador de CA ligado aos terminais de uma “caixa-preta”. A caixa contém um circuito R L C , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos.
Um dimmer típico, com os que são usados para regular a luminosidade das lâmpadas do palco nos teatros, é composto por um indutor variável L (cuja indutância pode ser ajustada entre zero e L m a x ) li
Um gerador de CA alimenta uam carga resistiva em uma fábrica distante através de uma linha de transmissão de dois cabos. Na fábrica, um transformador abaixador de tensão reduz a tensão do valor de tra