Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fasores e Circuitos RLC

Ver Teoria
Exercício 301234567891011121314151617181920212223242526272829313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Circuitos CA

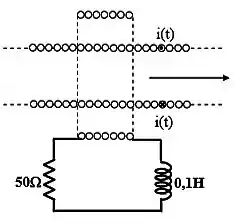
Num solenoide infinito passa uma corrente da forma i t = 10   s e n ω t A . Ela possui 100   e s p i r a s / m m e seu raio é de 20   c m . Uma bobina de 100 espiras e raio 30   c m é colocada de tal forma que seus eixos de simetria coincidem. Aos extremos da bobina é acoplado um resistor e um indutor conforme a figura (a indutância da bobina é desprezível).

  1. Calcule a força eletromotriz sobre a bobina.
  2. Calcule a corrente máxima que passa pelo circuito e o ângulo de fase entre a f e m e a corrente.
  3. Se colocarmos um capacitor no circuito, qual tem que ser o seu valor para que ele entre em ressonância?

Passo 1

Observe que o raio da bobina é maior que o do solenoide. Isso é de extrema importância, sabe por que? Porque assim, o campo magnético gerado pelo solenoide fica todo dentro da área da bobida. Lindo, não?

O fluxo do campo magnético gerado pelo solenoide é:

ϕ B = ∫ B → d A → = B A

ϕ B =   μ N i A s o l

ϕ B = 4 π ∙ 10 - 7 ∙ 100 ∙ 10 3 ∙ 10   s e n ω t ∙ π 0,2 2

ϕ B = 0,016 π 2 s e n ω t ≅ 0,16 s e n ( ω t )

Isto porque ele é homogêneo.

Agora vamos achar ω . A frequência é 60   H z , logo ω = 377   r a d / s .

Então,

ϕ B = 0,16   s e n ( 377 t )

Passo 2

Agora aplicamos a lei de Farday e:

E i n d = - N d ϕ B d t

E i n d = - 100 ∙ 0,16 ∙ 377 ∙ cos ⁡ 377 t

E i n d ≅ 6,0 ∙ 10 3 c o s ⁡ ( ω t )

Passo 3

Como só temos resistor e indutor,

i m á x = E m á x Z

Onde

Z = R 2 + X L 2

E

X L = ω L = 377 ∙ 0,1 = 37,7   Ω

Então,

Z = 50 2 + 37,7 2 = 63 Ω

E

i m á x = 6 ∙ 10 3 63 ≅ 100 A

Passo 4

Vamos direto a pergunta: qual a condição para ressonância?

ω = 1 L C

Logo,

C = 1 ω 2 L = 1 0,1 ∙ 377 2 = 7,5 ∙ 10 - 5 F

C = 75   μ F

Resposta

  1. E i n d = 6,0 ∙ 10 3 cos ⁡ ω t
  2. i m á x = 100   A
  3. C = 75   μ F

Exercícios de Livros Relacionados

Na Fig. 31-37, um gerador trifásico G produz energia elétrica que é transmitida através de três fios. Os potenciais dos três fios (em relação a uma referência comum) são V 1 = As e nω t para o fio 1,
Que corrente contínua produz a mesma energia térmica, em um certo resistor, que uma corrente alternada com um valor máximo de 2,60A ?
A figura 31-35 mostra um gerador de CA ligado aos terminais de uma “caixa-preta”. A caixa contém um circuito R L C , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos.
Um dimmer típico, com os que são usados para regular a luminosidade das lâmpadas do palco nos teatros, é composto por um indutor variável L (cuja indutância pode ser ajustada entre zero e L m a x ) li
Um gerador de CA alimenta uam carga resistiva em uma fábrica distante através de uma linha de transmissão de dois cabos. Na fábrica, um transformador abaixador de tensão reduz a tensão do valor de tra