Seja o circuito RLC em série mostrado na figura.
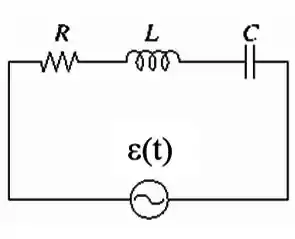
Considerando uma situação geral, com e qualquer, marque verdadeiro ou falso nas seguintes afirmações abaixo:
( ) A energia armazenada no circuito oscila entre e .
( ) A fonte não fornece potência ao circuito: a potência dissipada em é compensada pela variação da energia armazenada em e .
( ) A potência só é dissipada em .
( ) A corrente que passa no indutor está adiantada de e relação à d.d.p no mesmo indutor ().
( ) A tensão no capacitor está adiantada de em relação à tensão no resistor .
No caso das afirmações falsas explique, justificando, o porquê da sua afirmação.
Num dado instante de tempo, o diagrama de fasores do circuito é o seguinte:
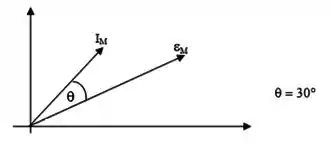
Utilizando apenas as informações do diagrama, calcule a tensão no resistor, .
Para que o circuito entre em ressonância, devemos aumentar ou diminuir a frequência do gerador?
Existe outro método (sem modificar ) que permita atingir a ressonância do circuito? Qual?
Passo 1
A primeira afirmação é verdadeira, em um circuito RLC, temos que a energia armazenada no mesmo oscila entre o indutor e o capacitor.
Passo 2
A segunda afirmação é falsa, pois a fonte fornece sim potência ao circuito, desse modo, a potência dissipada no resistor não é compensada pela variação da energia armazenada no indutor e no capacitor.
Passo 3
A terceira afirmação é verdadeira, dos componentes do circuito, apenas o resistor é capaz de dissipar a potência.
Passo 4
A quarta afirmação é falsa, a corrente está atrasada de em relação à d.d.p nos terminais do indutor.
Passo 5
A quinta afirmação é falsa, a tensão no capacitor está atrasada de em relação à tensão no resistor. Basta lembrar que a tensão no resistor está em fase com a corrente e esta está adiantada de em relação à tensão no capacitor.
Passo 6
Para achar o valor de , precisamos lembrar que a tensão no resistor está em fase com a corrente. Além disso, a soma vetorial de é igual à , logo, como a tensão no capacitor está atrasada de , e a tensão no indutor está adiantada de em relação à corrente, temos que a tensão no resistor será a componente de projetada sobre a corrente, ou seja:
Passo 7
Pelo diagrama, como a corrente está adianta em relação à tensão, podemos afirmar que o circuito é mais capacitivo, ou seja:
Para que o circuito entre em ressonância, precisamos que o valor de aumente enquanto diminua até se igualarem. Como é diretamente proporcional à , precisamos que a frequência do gerador aumente.
Passo 8
Sim, para atingir a ressonância sem modificar , devemos alterar o valor da indutância e da capacitância, pois, como as impedâncias também dependem desses valores, poderemos igualar seus valores se modificar a frequência do gerador:
No caso do circuito apresentado, por ser mais capacitivo, para que ele entre em ressonância, podemos aumentar o valor de ou diminuir o valor de .
Resposta
A frequência do gerador deve aumentar.
Sim. Devemos aumentar o valo de ou diminuir o valor de