Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fasores e Circuitos RLC

Ver Teoria
Exercício 241234567891011121314151617181920212223252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Circuitos CA

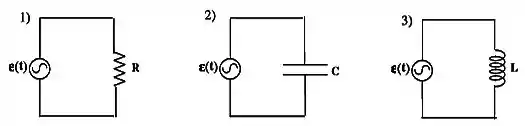
Uma fonte de corrente alternada, que tem a sua f e m variando no tempo da forma ε t = ε m   s e n ω t , é ligada a três elementos de circuito, como mostram as figuras abaixo.

Para cada um dos circuitos:

  1. Escreva a equação que relaciona a f e m da fonte com a corrente do circuito.
  2. Descreva a diferença de fase entre a f e m da fonte e a corrente do circuito.
  3. Ache corrente em função do tempo.

Passo 1

Primeiro vamos ver do que se trata cada item.

( 1 ) Circuito resistivo R

( 2 ) Circuito capacitivo C

( 3 ) Circuito indutivo L

Agora é só mostrar como calculamos a fem.

( 1 ) E = R i

( 2 ) E = Q / C

E = ∫ i d t / C

( 3 ) E = L d i / d t

Passo 2

Vamos fazer para cada um, de novo.

Para o circuito ( 1 ):

E t = E m s e n   ω t

i t = E m R s e n ( ω t )

Logo, estão em fase.

Passo 3

Para o circuito ( 2 ):

E t = E m s e n   ( ω t )

i t = d Q / d t

Onde

Q = C E t

Então,

i t = C E m ω c o s ⁡ ( ω t )

Logo, a diferença de fase entre a fonte e a corrente é π / 2 .

Passo 4

Para o circuito ( 3 ):

E t = E m s e n ω t

i t = ∫ E t d t L = ∫ E m s e n ω t L d t

i ( t ) = E m ω L - cos ⁡ ω t

Logo, a diferença de fase entre a fonte e a corrente é de π / 2 .

Passo 5

Achar a corrente em função do tempo já está foi feito nos passos 2 , 3 e 4 .

Resposta

  1. ( 1 )   E = R i  

    2. ( 2 ) E = ∫ i d t / C

    ( 3 ) E = L d i / d t

  2. ( 1 ) 0

    3. ( 2 ) π / 2

    ( 3 ) π / 2

  3. ( 1 ) i t = E m s e n ( ω t ) / R

( 2 ) i t = ω C E m c o s ( ω t )

( 3 ) i t = - E m c o s ⁡ ( ω t ) / ω L

Exercícios de Livros Relacionados

Na Fig. 31-37, um gerador trifásico G produz energia elétrica que é transmitida através de três fios. Os potenciais dos três fios (em relação a uma referência comum) são V 1 = As e nω t para o fio 1,
Que corrente contínua produz a mesma energia térmica, em um certo resistor, que uma corrente alternada com um valor máximo de 2,60A ?
A figura 31-35 mostra um gerador de CA ligado aos terminais de uma “caixa-preta”. A caixa contém um circuito R L C , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos.
Um dimmer típico, com os que são usados para regular a luminosidade das lâmpadas do palco nos teatros, é composto por um indutor variável L (cuja indutância pode ser ajustada entre zero e L m a x ) li
Um gerador de CA alimenta uam carga resistiva em uma fábrica distante através de uma linha de transmissão de dois cabos. Na fábrica, um transformador abaixador de tensão reduz a tensão do valor de tra