O circuito em série mostrado na Figura 1 é alimentado pela fonte de corrente alternada onde , , , , e .
Determine os valores de e , assim como dos valores máximos das tensões no resistor, indutor e capacitor.
Com base nestes valores, represente o diagrama fasorial para o circuito, indicado se ele é indutivo ou capacitivo.
Em seguida, suponha que a mesma fonte , onde e , é conectada a um outro circuito série com , , fixos mas desconhecidos. Quando , medem-se e . Quando , medem-se e .
Com base nos dados fornecidos imediatamente acima determine os valores de , e .
Passo 1
Determine os valores de e , assim como dos valores máximos das tensões no resistor, indutor e capacitor.
As tensões máximas no resistor, indutor e no capacitor são dadas por:
Onde:
Então precisamos começar calculando , , e .
Os dados do problema são:
Logo:
Agora podemos calcular e as voltagens máximas.
Passo 2
O problema também pede para calcularmos a diferença de fase , que é dada por:
Passo 3
Com base nestes valores, represente o diagrama fasorial para o circuito, indicado se ele é indutivo ou capacitivo.
Como estamos trabalhando com um circuito , precisamos lembrar de algumas coisas:
- A tensão no resistor e a corrente estão em fase, ou seja, o ângulo de rotação do fasor é o mesmo de .
- A corrente está adiantada em relação à tensão no capacitor, ou seja, o ângulo de rotação do fasor é o mesmo da corrente menos .
- A corrente está atrasada em relação à tensão no indutor, ou seja, o ângulo de rotação no fasor é o mesmo da corrente mais .
Assim, o diagrama fasorial terá essa cara:
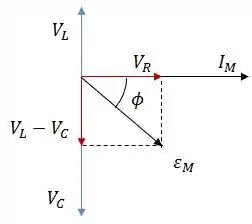
Como , o diagrama é capacitivo.
Passo 4
Com base nos dados fornecidos imediatamente acima determine os valores de , e .
O problema diz que, quando , e .
Se a diferença de fase é nula, corresponde à frequência de ressonância, logo, para :
Além disso, na ressonância, , logo:
Passo 5
Para , medem-se e .
Daqui podemos tirar que:
Do passo anterior, descobrimos que e . E, de acordo com o enunciado, , logo:
Agora podemos descobrir, também, , usando a frequência de ressonância:
Portanto:
Resposta
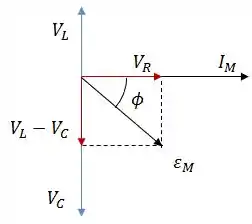
O diagrama é capacitivo.