Um indutor ideal, de indutância desconhecida não nula, um resistor de resistência e um capacitor ajustável conectados em série a uma fonte de tensão alternada . A amplitude da corrente circulando no circuito quando o capacitor é ajustado para o valor é a mesma de quando o capacitor é ajustado para o valor .

Determine em função dos parâmetros dados:

(a) A indutância do indutor

(b) A amplitude da corrente no circuito

(c) A fase em relação à fonte de tensão quando o capacitor vale e

(d) A potência média dissipada no circuito qunado o capacitor vale

Agora que descobrimos a indutância, para descobrir a corrente, basta usar

Como

e

(Aqui tanto faz usar a capacitância de ou já que as duas produzem a mesma corrente!)

Temos finalmente

E é isso. Não fica mais bonito não, mas tá certo ;)

Temos que lembrar que a fase da corrente em relação à fonte é relacionada por

No caso em que a condutância vale

No caso em que a condutância vale

A potência média é dada por

Substituindo a amplitude da corrente e a fase, que já achamos

Calma que eu segurei esse ! Substituir logo daria um negócião gigante! Vou te ensinar um macete pra calcular o cosseno de arcotangente ;)

Temos que o nosso ângulo é dado por

Aqui tanto faz escolher a solução para com sinal de menos ou mais por que a função cosseno é uma função par (. Para deixar mais simples, escolhi a solução com o argumento do arcotangente positivo.

Até aí, nada de novo. Mas a gente consegue pensar em uma coisa: sabemos que a tangente é o cateto oposto dividido pela hipotenusa, certo? E se a gente desenhar um triângulo retângulo cujos catetos sejam e ? Ficaria algo tipo assim:

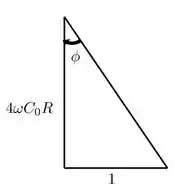
Ah maneiro! Agora só preciso da hipotenusa para calcular o cosseno de . Pra isso basta usar Pitagorás! A hipotenusa será

Assim temos

Pra deixar com a cara da nossa expressão da potência, vamos dividir o numerador e o denominador por

Assim, voltando para a potência média