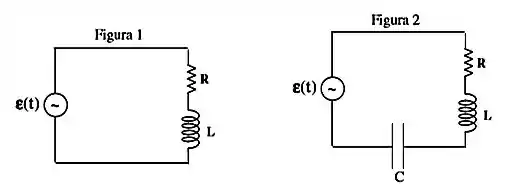
O circuito elétrico de uma fábrica por ser representado, basicamente, pelo circuito da figura . As máquinas, que tem motores feitos de bobinas e também consomem energia, são representadas por elementos indutivos e resistivos. Em uma determinada fábrica, a fonte de corrente alternada possui uma amplitude de e uma frequência de ciclos de . A resistência equivalente de todas as máquinas é de e sua indutância equivalente é .
Obs.: Note que é zero nesse circuito.
- Calcule a amplitude de corrente e a diferença de fase entre a corrente e a tensão da fonte.
- Obtenha a potência média fornecida pela fonte e a potência média dissipada na resistência.
- Para ter eficiência máxima, qual deve ser o valor da capacitância do capacitor da figura ?
A operadora disponibiliza para fábrica uma potência média dada por . Para que a potência consumida pela fábrica (na resistência) tenha maior eficiência possível, isto é, seja a mesma fornecida pela operadora, instalam-se capacitores na sua linha, como mostrado na figura através de um capacitor equivalente.
Passo 1
Primeira coisa que devemos observar é que não temos capacitor, logo .
Para o indutor, temos:
Agora podemos calcular a impedância, substituindo os valores:
Passo 2
Pronto! Agora substituímos os valores para achar a corrente:
Passo 3
Agora, vamos calcular a diferença de fase entre a corrente e a tensão da fonte:
Passo 4
Bem, agora é aplicação de fórmula, visto que já temos todos os valores necessários para calcular potências.
Potência fornecida pela fonte:
Potência dissipada na resistência:
Passo 5
Para finalizar a questão, vamos calcular o valor da capacitância no caso de eficiência seja máxima. Para que isto ocorra, é necessário que o circuito esteja em ressonância.
Ressônancia te lembra o que?
Como queremos achar a capacitância,
Resposta