Um circuito ligado a uma fonte de corrente alternada é mostrado na Figura abaixo. Este circuito se encontra em ressonância e apresenta uma voltagem eficaz (rms) de .
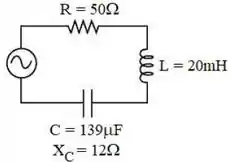
1) Qual é o valor da frequência de oscilação do gerador de corrente alternada que está ligado ao circuito?
(a)
(b)
(c)
(d)
(e)
2) Qual é o valor da impedância deste circuito?
(a)
(b)
(c)
(d)
(e)
3) Qual é o valor da corrente máxima que circula neste circuito?
(a)
(b)
(c)
(d)
(e)
4) O circuito da figura apresenta características:
(a) resistivas, pois os valores para as reatâncias indutiva e capacitiva são iguais.
(b) indutivas, pois a reatância indutiva apresenta um valor maior que a reatância capacitiva.
(c) indutivas, pois a constante de fase é positiva.
(d) capacitivas, pois a reatância indutiva apresenta um valor menor que a reatância capacitiva.
(e) capacitivas, pois a constante de fase é negativa.
5) Qual dentre os diagramas de fasores apresentados abaixo melhor representa a relação entre os fasores para a voltagem em cada elemento do circuito?
(a) 
(b) 
(c) 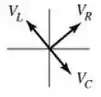
(d) 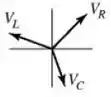
(e) 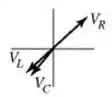
Passo 1
Sabemos, que na ressonância,
Pra fazer essa continha sem calculadora fica interessante fazer assim
Agora vamos elevar tudo ao quadrado pra tentar tirar a raiz quadrada só no final
Se você multiplicar vai achar . Como queremos um valor aproximado vou aproximar essa multiplicação por . Na guerra e na múltipla escolha vale tudo!
Agora sim, tirando a raiz quadrada
Aí agora não tem pra onde fugir.... a gente sabe que . E raiz de ? Se você não lembra (pode chutar também xD), assim como é muito perto de , então é quase ! Assim
Passo 2
Como o circuito está em ressonância, sua impedância será dada por:
Passo 3
A corrente máxima que circula no circuito é dada por:
Bem, sabemos que e que . Logo,
Passo 4
Como o circuito está em ressonância, as reatâncias indutiva e capacitiva, e , são iguais, . Assim sendo, o circuito apresenta características resistivas.
Passo 5
Vamos lá:
- Circuito está em ressonância, certo? Logo, .
- Capacitor e indutor estão em série... isso significa que a mesma corrente passa por eles.
- Assim sendo, , como podemos ver nos fasores representados no item (c).
Resposta
1) (a)
2) (a)
3) (e)
4) (a) resistivas, pois os valores para as reatâncias indutiva e capacitiva são iguais.
5) (c)