Depois de medir a autoindutância de uma bobina, você a desenrola e então enrola metade do comprimento do fio em outra bobina com o mesmo diâmetro e mesmo comprimento, mas com a metade do número de espiras. Com esta ação, a autoindutância:
- Reduz-se a da anterior
- É a mesma
- Dobra
- Reduz-se à metade da anterior
- Quadruplica
Passo 1
Cara, uma bobina tem essa cara aqui...
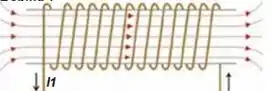
De acordo com a teoria, podemos encontrar o valor da autoindutância , sabendo que existe uma relação do fluxo concatenado pela bobina com a autoindutância...
Então basta encontrar qual é a cara desse fluxo que depois está resolvido o nosso problema.
Passo 2
Repare que o campo magnético criado pelo solenoide gera um fluxo de campo dentro do própria bobina. Esse luxo é e pode ser encontrado pegando o fluxo de uma única espira...
E depois multiplicando pelo fluxo gerado por espiras que contém a nossa bobina...
Além disso, repare que o campo magnético é sempre paralelo ao vetor de área . Esse paralelismo nos permite falar que e, portanto...
Veja aqui que o campo é sempre uniforme dentro do solenoide, ou seja, possui o mesmo valor em todos os pontos da espira, portanto, não se varia com a posição da área dentro...
A integral de é a área de uma espira do solenoide...
Como vimos, o campo magnético do solenoide pode ser calculado por...
Ou seja...
Repare que podemos rearranjar da seguinte forma...
E o que isso nos revela sobre a autoindutância?
Passo 3
Bem, nos revela que a autoindutância de uma bobina vale...
Ou seja, se a gente enrola o fio em outra bobina de mesmo diâmetro (portanto mesmo raio ) e mesmo comprimento , mas com a metade do número de espiras, ou seja, , a nossa nova indutância vai cair...
Ou seja, a indutância da bobina se reduz !
Resposta
Letra A