Um indutor real é formado por uma indutância e uma resistência em série, como mostrado na figura:
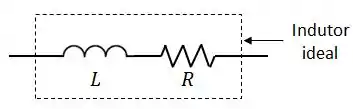
Antes de montar um circuito, queremos descobrir os valores de e . Para isso, conectamos inicialmente o indutor real a uma fonte de tensão contínua de . Após ter esperado um tempo suficientemente longo, medimos, utilizando um multímetro, uma corrente .
Em seguida, conectamos o mesmo indutor real a um gerador de tensão alternada de valor quadrático médio, e com frequência angular . Neste caso, medimos uma corrente quadrática média, .
De posse destas informações determine os valores de e (com os valores numéricos e as unidades).
Em seguida, um capacitor é conectado em série ao indutor real, formando assim um circuito . Este circuito é conectado ao mesmo gerador de tensão alternada do item anterior.
Utilizando os dados à sua disposição, desenhe, nesta condição, o diagrama de fasores do circuito. O circuito tem comportamento capacitivo ou indutivo?
Passo 1
De posse destas informações determine os valores de e (com os valores numéricos e as unidades).
De acordo com o enunciado, após conectar o indutor real a uma fonte de tensão contínua de e esperar um tempo suficientemente longo, a corrente medida foi de .
Em um circuito , a corrente varia com o tempo de acordo com a equação:
Quando o problema diz “após um tempo suficientemente longo”, ele que dizer “quando ”.
Nesse caso, quando :
Passo 2
Após conectar o indutor real a um gerador de tensão alternada de e , mediu-se .
A tensão está associada à corrente por:
Onde é a impedância, definida por:
Como não temos capacitor nesse circuito :
Onde é a reatância indutiva, definida por .
Opa! Daqui vamos conseguir chegar ao valor de , então vamos continuar:
De acordo com o enunciado, .
Finalmente:
Passo 3
Utilizando os dados à sua disposição, desenhe, nesta condição, o diagrama de fasores do circuito. O circuito tem comportamento capacitivo ou indutivo?
As tensões resistiva, indutiva e capacitiva são dadas por:
Sabendo que a tensão indutiva está adiantada de e que a tensão indutiva está atrasada de , o diagrama de Fasores será:
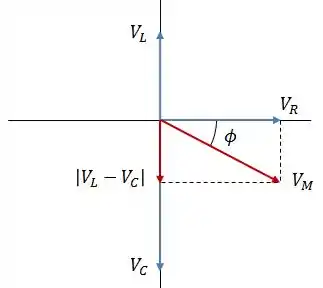
Como , o circuito tem comportamento capacitivo.
Resposta
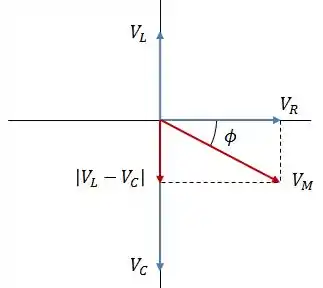
O circuito tem comportamento capacitivo.