UFRJ, Cálculo 4, P5 2020, Questão 9
Considere o problema da corda vibrante dado por , , com as condições de contorno e as condições iniciais e
Nessas condições, o gráfico que melhor representa a solução no instante é
Passo 1
Esse é o gráfico que representa melhor a solução...
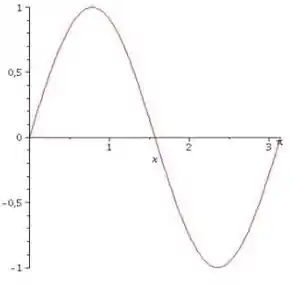
Por ter o , é necessários que nos pontos e , o valor do gráfico seja igual a .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Os Problemas 19 e 20 indicam como é possível mostrar que a solução formal (20), (22) das Eqs. (1), (3) e (9) é, de fato, a solução desse problema.19- Usando a identidade trigonométrica s e nAc o sB=½
Seja h ( ξ ) o deslocamento inicial em [ 0 ,L ] estendido a ( - L ,0 ) como uma função ímpar e estendido ao resto da reta como uma função periódica de período 2 L . Supondo a continuidade de h e suas
Combinando os resultados dos Problemas 16 e 17, mostre que a solução do problemaé dada por
O movimento de uma membrana circular elástica, como a membrana de um tambor, é determinado pela equação de onda bidimensional em coordenadas polaresSupondo que u ( r ,θ ,t )=R r Θ ( θ ) T ( t ) , enco
Considere a equação de onda a 2 u x x = u t t em um meio unidimensional infinito, sujeita às condições iniciaisUsando a forma da solução obtida no Problema 13, mostre queUse a primeira das equações no