Questão 4:
Vamos considerar a corda de um violão tocada puxando-a com perfil inicial e soltando-a sem velocidade inicial . O movimento ideal da corda elástica sem amortecimento é dado pela solução da equação da onda unidimensional
Com as condições de contorno das extremidades . Se
A solução do problema acima é dada pela série:
A série converge? Para qualquer e ? Explique e justifique.
Passo 1
A série converge para dentro de e . Para justiçar isso, venha comigo nesse passo-a-passo!
Passo 2
Primeiro, vamos pontuar aqui algumas considerações iniciais importantes sobre essa corda:
- Primeiro: é uma corda de um violão, portanto contínua (pelo menos no estado inicial, basta observar que é contínua para qualquer ponto de no intervalo de a ).
- Sabe-se que para qualquer valor de as pontas estão amarradas .
Com essas condições iniciais, conseguimos traçar um perfil da corda inicialmente:
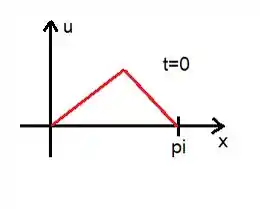
Esses dados iniciais servem para mostrar que pelo menos no estante inicial e nas pontas em qualquer instante a série tem que convergir com certeza.
Passo 3
Agora, olhemos para a série que representa a corda:
E suponha por absurdo que existe algum ponto no interior da corda que divirja (meio doido isso só de olhar pra corda, neh, pois pra ela divergir com as duas pontas amarradas no , só se ela começar a esticar no meio pro infinito e sem arrebentar). Mas, ok, por absurdo existe esse ponto que vai pro infinito (a soma diverge).
Pow, a série que representa esse ponto intrigante é esse daqui:
Essa é uma série alternada e com e conhecidos, podemos arrumar a série alternada assim:
e que, portanto converge sempre que:
- O termo entre colchetes vai a no infinito.
- O termo entre parênteses seja positivo.
Pow, se o cosseno e o seno forem simultaneamente positivos ou negativos, o produto será independente positivo. Um cara positivo, dividido por um numero ao quadrado? SIM! Isso gera um cara positivo!
Além disso, como o seno e o cosseno são funções limitadas, no infinito (quanto aumenta), esse termo dos colchetes só pode ir ao zero!
Caso o seno e o cosseno não sejam simultaneamente positivos ou negativos, o produto gerará um menos que pode se juntar com o virando um e o produto se torna positivo e decrescente como deve ser para a série convergir. O que nos leva a seguinte conclusão:
A série converge independente do e que estamos falando, logo o absurdo da série divergir nesse ponto, é de fato um absurdo, ou seja, ela converge para qualquer e (claro que precisa estar dentro do intervalo de a que é onde se faz sentido ter corda).
Resposta
A série converge para dentro de e .