Listas de Física 2 - Profº Eduardo Duzzioni de Física 2 da UFSC - Lista de Exercícios 1
Física 2 - UFSC
1) Um mergulhador realiza ao saltar de uma plataforma de . Supondo que a velocidade vertical inicial seja nula, determine a velocidade angular média do mergulhador.
Ver solução completa2) Quando se deixa cair uma fatia de pão com manteiga de uma mesa, a fatia adquire um movimento de rotação. Se a distância da mesa ao chão é de e para rotações menores que , determine (a) a menor velocidade angular para qual a fatia cai com a manteiga para baixo.
Ver solução completa2) Quando se deixa cair uma fatia de pão com manteiga de uma mesa, a fatia adquire um movimento de rotação. Se a distância da mesa ao chão é de e para rotações menores que , determine (b) a maior velocidade angular para qual a fatia cai com a manteiga para baixo.
Ver solução completa3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos. Em , qual é (a) a posição angular do ponto.
Ver solução completa3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos. Em , qual é (b) sua velocidade angular?
Ver solução completa3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos.
(c) Qual é a velocidade angular em ?
Ver solução completa3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos.
(d) calcule a aceleração em ?
Ver solução completa3) A posição angular de um ponto em uma roda é dada por , onde está em radianos e em segundos.
(e) A aceleração angular da roda é constante? Explique.
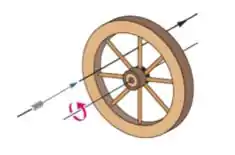
Ver solução completa4) A roda da figura tem oito raios de igualmente espaçados, está montada em um eixo fixo e gira a . Você deseja atirar uma flecha de de comprimento paralelamente ao eixo da roda sem atingir um dos raios. Suponha que a flecha e os raios são muito finos. (a) Qual é a menor velocidade que a flecha deve ter?
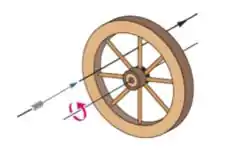
4) A roda da figura tem oito raios de igualmente espaçados, está montada em um eixo fixo e gira a . Você deseja atirar uma flecha de de comprimento paralelamente ao eixo da roda sem atingir um dos raios. Suponha que a flecha e os raios são muito finos. (b) O ponto entre o eixo e a borda da roda por onde a flecha passa faz alguma diferença? Caso a resposta seja afirmativa, para que ponto você deve mirar?
5) Um disco, inicialmente girando a , é freado com uma desaceleração angular constante de módulo . (a) Quanto tempo o disco leva para parar?
Ver solução completa5) Um disco, inicialmente girando a , é freado com uma desaceleração angular constante de módulo . (b) Qual é o deslocamento angular total descrito pelo disco durante esse tempo?
Ver solução completa6) Um tambor gira em torno de seu eixo central com uma velocidade angular de . Se o tambor é freado a uma taxa constante de , (a) quanto tempo leva para parar?
Ver solução completa6) Um tambor gira em torno de seu eixo central com uma velocidade angular de . Se o tambor �� freado a uma taxa constante de , (b) Qual é o deslocamento angular total descrito pelo tambor até parar?
Ver solução completa7) Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em . (a) Qual é o maior ângulo descrito pela reta de referência no sentido positivo?
Ver solução completa7) Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em Quais são (b) o primeiro e (c) o segundo instante no qual a reta de referência passa pelo ângulo ?
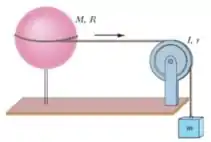
Ver solução completa7) Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em Quais são (d) instante negativo e (e) instante positivo a reta de referência passa pelo ângulo ?
Ver solução completa7) Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em (f) Faça um gráfico de em função de e indique as respostas dos itens (a) a (e) no gráfico.
Ver solução completa8) Um disco gira em torno do seu eixo central partindo do repouso com aceleração angular constante. Em um certo instante ele está girando a ; após revoluções, sua velocidade angular é de . Calcule (a) a aceleração angular.
Ver solução completa8) Um disco gira em torno do seu eixo central partindo do repouso com aceleração angular constante. Em um certo instante ele está girando a ; após revoluções, sua velocidade angular é de . Calcule (b) o tempo necessário para completar revoluções.
Ver solução completa8) Um disco gira em torno do seu eixo central partindo do repouso com aceleração angular constante. Em um certo instante ele está girando a ; após revoluções, sua velocidade angular é de . Calcule (c) o tempo necessário para atingir a velocidade angular de .
Ver solução completa8) Um disco gira em torno do seu eixo central partindo do repouso com aceleração angular constante. Em um certo instante ele está girando a ; após revoluções, sua velocidade angular é de . Calcule (d) o número de revoluções desde o repouso até o instante em que o disco atinge a velocidade angular de .
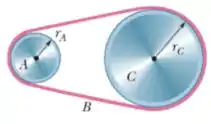
Ver solução completa11) Na figura abaixo uma roda de raio está acoplada por uma correia a uma roda de raio . A velocidade angular da roda é aumentada a partir do repouso a uma taxa constante de . Determine o tempo necessário para que a roda atinja uma velocidade angular de , supondo que a correia não deslize.
12) Calcule o momento de inércia de uma roda que tem uma energia de quando gira a
Ver solução completa9) Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, ao partir, gira de acordo com a equação , onde está em segundos e em radianos. Quando , quais são os módulos (a) da velocidade angular.
Ver solução completa9) Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, ao partir, gira de acordo com a equação , onde está em segundos e em radianos. Quando , quais são os módulos (b) da velocidade linear
Ver solução completa9) Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, ao partir, gira de acordo com a equação , onde está em segundos e em radianos. Quando , quais são os módulos (c) da aceleração tangencial
Ver solução completa9) Um astronauta está sendo testado em uma centrífuga. A centrífuga tem um raio de e, ao partir, gira de acordo com a equação , onde está em segundos e em radianos. Quando , quais são os módulos (d) da aceleração radial do astronauta?
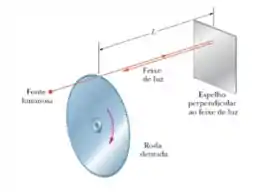
Ver solução completa10) Um método para medir a velocidade da luz usa uma roda dentada giratória. Um feixe de luz passa pelo espaço entre dois dentes situados na borda da roda, viaja até um espelho distante e chega de volta à roda exatamente a tempo de passar pelo espaço seguinte entre dois dentes. Uma dessas rodas tem de raio e entre dentes. Medidas realizadas quando o espelho está a uma distância da roda fornecem o valor de para a velocidade da luz. (a) Qual é a velocidade angular (constante) da roda?
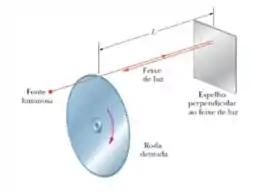
10) Um método para medir a velocidade da luz usa uma roda dentada giratória. Um feixe de luz passa pelo espaço entre dois dentes situados na borda da roda, viaja até um espelho distante e chega de volta à roda exatamente a tempo de passar pelo espaço seguinte entre dois dentes. Uma dessas rodas tem de raio e entre dentes. Medidas realizadas quando o espelho está a uma distância da roda fornecem o valor de para a velocidade da luz. (b) Qual é a velocidade linear de um ponto na borda da roda?
13) Calcule o momento de inércia de uma régua de um metro, com uma massa de , em relação a um eixo perpendicular à régua na marca de . Trate a régua como uma barra fina.
Ver solução completa14) Dois cilindros uniformes, ambos girando em torno do eixo central (longitudinal) com uma velocidade angular de , têm a mesma massa de e raios diferentes. Qual é a energia cinética de rotação (a) do cilindro menor, de raio
Ver solução completa14) Dois cilindros uniformes, ambos girando em torno do eixo central (longitudinal) com uma velocidade angular de , têm a mesma massa de e raios diferentes. Qual é a energia cinética de rotação (b) do cilindro maior, de raio ?
Ver solução completa15) Alguns caminhões utilizam a energia armazenada em um volante que um motor elétrico acelera até uma velocidade de . Um desses volantes é um cilindro uniforme com uma massa de e um raio de . (a) Qual é a energia cinética máxima do volante quando está girando com a velocidade máxima?
Ver solução completa15) Alguns caminhões utilizam a energia armazenada em um volante que um motor elétrico acelera até uma velocidade de . Um desses volantes é um cilindro uniforme com uma massa de e um raio de . (b) Se o caminhão consome uma potência média de , por quantos minutos pode operar sem que o volante seja novamente carregado?
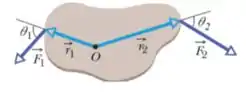
Ver solução completa16) O corpo da figura abaixo pode girar em torno de um eixo perpendicular ao plano do papel passando por , e duas forças atuam sobre ele, como mostra a figura. Se , , , , e , qual é o torque resultante em relação ao eixo?
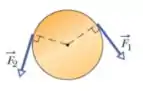
17) A figura abaixo mostra um disco homogêneo que pode girar em torno do centro como um carrossel. O disco tem raio de e massa de , e está inicialmente em repouso. A partir do instante , duas forças devem ser aplicadas tangencialmente à borda do disco, como mostra a figura, para que, no instante , o disco tenha uma velocidade angular de no sentido anti-horário. A força tem um módulo de . Qual é o módulo de ?
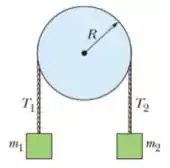
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos?
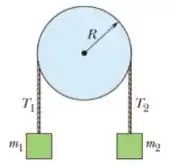
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. Qual é o valor (b) da tensão .
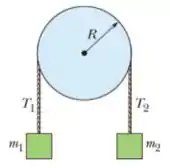
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. Qual é o valor (c) da tensão ?
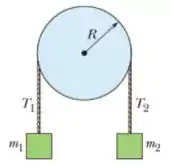
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. (d) Qual é o módulo da aceleração angular da polia?
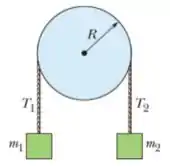
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. (e) Qual é o momento de inércia da polia?
19) Uma roda de , essencialmente um aro fino com de raio, está girando a . Ela precisa ser parada em . (a) Qual é o trabalho necessário para fazê-la parar?
Ver solução completa19) Uma roda de , essencialmente um aro fino com de raio, está girando a . Ela precisa ser parada em . (b) Qual é a potência média necessária?
Ver solução completa20) Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremidade de apoio não escorrega.
Ver solução completa21) Uma casca esférica uniforme de massa e raio pode girar em torno de um eixo vertical sem atrito. Uma corda de massa desprezível está enrolada no equador da casca, passa por uma polia com momento de inércia e raio e está presa a um bloco de massa . Não há atrito no eixo da polia e a corda não escorrega na casca nem na polia. Qual é a velocidade do bloco depois de cair após ter sido liberado do repouso?