UFSC, Sem Campus, Física 2, Listas de Física 1 - Profº Eduardo Duzzioni - Lista de Exercícios 1, Questão 18e.
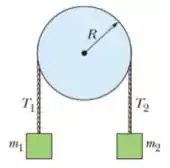
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. (e) Qual é o momento de inércia da polia?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos que obter o momento de inercia da polia.
Como vamos fazer isso? 🤔
Pra isso, podemos aplicar a formula que relaciona o torque resultante e o momento de inércia.
Como temos as trações da corda, podemos obter o torque resultante e como também temos a aceleração angular, podemos simplesmente substituir na equação que é dada por
Mas torque é o produto da força com a distancia onde ela é aplicada, ou seja
Sacou como fazemos isso? 😉
Passo 2
Como no enunciado que o bloco cai, então podemos dizer que o torque resultante é dado por
Igualando as duas equações de ...
Isolando , temos
Se foi dado como , e foram calculados anteriormente como e respectivamente e foi calculado como . Substituindo em
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
