Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade e Aceleração Médias no Movimento Circular

Ver Teoria
Exercício 5612345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455575859606162636465

Enunciado

UFSC, Sem Campus, Física 2, Listas de Física 1 - Profº Eduardo Duzzioni - Lista de Exercícios 1, Questão 10a.

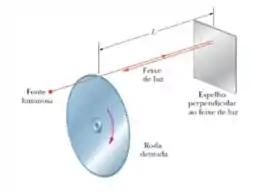
10) Um método para medir a velocidade da luz usa uma roda dentada giratória. Um feixe de luz passa pelo espaço entre dois dentes situados na borda da roda, viaja até um espelho distante e chega de volta à roda exatamente a tempo de passar pelo espaço seguinte entre dois dentes. Uma dessas rodas tem 5,0   c m de raio e 500   e s p a ç o s entre dentes. Medidas realizadas quando o espelho está a uma distância L = 500 m da roda fornecem o valor de 3 · 10 5 k m / s para a velocidade da luz. (a) Qual é a velocidade angular (constante) da roda?

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão queremos obter a velocidade angular de um disco serrilhado em que um feixe de luz passa por uma fresta na sua borda, reflete em um espelho a L = 500 m de distância e volta passando da fresta seguinte.

Dado que o disco tem 5   c m de raio e 500 espaços entre os dentes, como podemos fazer isso? 🤔

A velocidade angular de um disco é dada pela variação do movimento angular ∆ θ sobre o intervalo de tempo desse movimento, ou seja

ω = ∆ θ ∆ t

Portanto, temos que obter o deslocamento angular do disco do momento em que o feixe passa pela primeira fresta até voltar na fresta seguinte.

E depois obter o tempo em que isso ocorre dado que a velocidade da luz é 3 · 10 5 k m / s e L = 500 m .

Sacou? Bora começar! 😁

Passo 2

Primeiro vamos obter o deslocamento angular do disco

Se 2 π   r a d corresponde a uma volta inteira e a borda do disco tem 500 frestas, então a distância entre uma fresta e outra é dada por

∆ θ = 2 π 500 = 12,57 · 10 - 3   r a d

Agora se o tempo desse movimento é o mesmo tempo de o feixe de luz leva para sair do disco, refletir em um espelho a 500 m e voltar para o disco, ou seja, pela equação da velocidade linear, temos

v = ∆ S ∆ t → ∆ t = ∆ S v

Se 1   k m = 1000   m , então 3 · 10 5 k m / s = 3 · 10 8 m / s

∆ t = 2 500 3 · 10 8 = 3,33 · 10 - 6 s

Por fim, substituindo na fórmula do movimento angular, temos

ω = ∆ θ ∆ t = 12,57 · 10 - 3 3,33 · 10 - 6

ω = 3771   r a d / s

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

ω = 3771   r a d / s

Exercícios de Livros Relacionados

Pulsares são estrelas de nêutrons que emitem raios X e outras radiações de tal forma que nós, na Terra, recebemos pulsos de radiação dos pulsares em intervalos regulares iguais ao período de sua rotaç
Um próton sujeito a um campo magnético realiza um movimento helicoidal uniforme, com os seguintes parâmetros v x y = 5,00 x 10 5 m / s , a = 4,00 x 10 12 m / s 2 e v z = 2,00 x 10 4 m / s . Calcule o
As lâminas de um ventilador giram com velocidade angular dada por ω z t = γ - β t 2 , onde γ = 5r a d / s e β = 0,8r a d / s 3 . a) Calcule a aceleração angular em função do tempo. b) Calcule a aceler
Uma criança está empurrando um carrossel. O deslocamento angular do carrossel varia com o tempo de acordo com a relação θ t = γ t + β t 3 , onde γ = 0,4r a d / s e β = 0,012r a d / s 3 .a) Calcule a v
Uma roda gira em torno de um eixo que está na direção z . A velocidade angular ω z é - 6 rad/s para t = 0 , aumenta linearmente no decorrer do tempo e é + 8 rad/s para t = 7 s. Consideramos a rotação