Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade e Aceleração Médias no Movimento Circular

Ver Teoria
Exercício 4212345678910111213141516171819202122232425262728293031323334353637383940414344454647484950515253545556575859606162636465

Enunciado

UFSC, Sem Campus, Física 2, Listas de Física 1 - Profº Eduardo Duzzioni - Lista de Exercícios 1, Questão 7f.

7) Em t = 0 , uma roda tem uma velocidade angular de 4,7   r a d / s , uma aceleração angular constante de - 0,25   r a d / s 2 e uma reta de referência em θ 0 = 0 (f) Faça um gráfico de θ em função de t e indique as respostas dos itens (a) a (e) no gráfico.

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema temos uma roda que possui uma velocidade angular inicialmente de 4,7   r a d / s e possui uma aceleração de - 0,25   r a d / s 2 .

Dado uma reta de referência em θ 0 = 0   r a d , como podemos esboçar o gráfico de θ em função de t ? 🤔

Lembra do movimento retilíneo que a fórmula da velocidade uniformemente variável é dada por

S = S 0 + v 0 t + a t 2 2

No caso do movimento circular, a ideia é muito parecida, só que no caso de v , temos ω , a será o α e S será θ , ou seja

θ = θ 0 + ω 0 t + α t 2 2

Bora começar!

Passo 2

No caso, θ 0 = 0   r a d , θ = - 10,5   r a d , ω 0 = 4,7   r a d / s , α = - 0,25   r a d / s 2 e t é o valor que procuramos

Substituindo na equação do movimento

θ = θ 0 + ω 0 t + α t 2 2

θ = 0 + 4,7 t - 0,25 t 2 2

θ t = 4,7 t - 0,125 t 2

Essa é a função que temos que esboçar.

Pelo que podemos lembrar de cálculo, essa função é um paraboloide com a concavidade voltada para baixo devido ao termo de maior grau ser negativo.

Podemos obter as raízes de θ t como

θ t = 4,7 t - 0,125 t 2 = 0

t 4,7 - 0,125 t = 0

t 1 = 0 t 2 = 4,7 0,125 = 37,6

Assim, como calculamos que o ponto máximo de θ é 44,18   r a d , podemos esboçar o gráfico

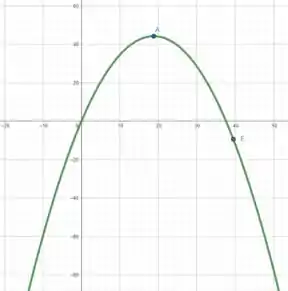
Fim! Iae, o que achou? Responde Aí! 😁

Resposta

θ t = 4,7 t - 0,125 t 2

Exercícios de Livros Relacionados

Pulsares são estrelas de nêutrons que emitem raios X e outras radiações de tal forma que nós, na Terra, recebemos pulsos de radiação dos pulsares em intervalos regulares iguais ao período de sua rotaç
Um próton sujeito a um campo magnético realiza um movimento helicoidal uniforme, com os seguintes parâmetros v x y = 5,00 x 10 5 m / s , a = 4,00 x 10 12 m / s 2 e v z = 2,00 x 10 4 m / s . Calcule o
As lâminas de um ventilador giram com velocidade angular dada por ω z t = γ - β t 2 , onde γ = 5r a d / s e β = 0,8r a d / s 3 . a) Calcule a aceleração angular em função do tempo. b) Calcule a aceler
Uma criança está empurrando um carrossel. O deslocamento angular do carrossel varia com o tempo de acordo com a relação θ t = γ t + β t 3 , onde γ = 0,4r a d / s e β = 0,012r a d / s 3 .a) Calcule a v
Uma roda gira em torno de um eixo que está na direção z . A velocidade angular ω z é - 6 rad/s para t = 0 , aumenta linearmente no decorrer do tempo e é + 8 rad/s para t = 7 s. Consideramos a rotação