Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação da Energia Mecânica

Ver Teoria
Exercício 100123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

UFSC, Sem Campus, Física 2, Listas de Física 1 - Profº Eduardo Duzzioni - Lista de Exercícios 1, Questão 21.

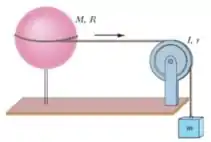
21) Uma casca esférica uniforme de massa M = 4,5 k g e raio R = 8,5 c m pode girar em torno de um eixo vertical sem atrito. Uma corda de massa desprezível está enrolada no equador da casca, passa por uma polia com momento de inércia I = 3,0 · 10 - 3 k g . m 2 e raio r = 5,0 c m e está presa a um bloco de massa m = 0,60 k g . Não há atrito no eixo da polia e a corda não escorrega na casca nem na polia. Qual é a velocidade do bloco depois de cair 82   c m após ter sido liberado do repouso?

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema temos uma casca esférica de massa M = 4,5   k g e raio R = 8,5 c m , uma polia de momento de inercia I p = 3,0 · 10 - 3 k g . m 2 e raio r = 5 c m e um bloco de massa m = 0,6 k g . O bloco cai 82 c m e queremos saber qual é a velocidade do bloco após essa queda.

Tem ideia de como fazemos isso? 🤔

Aqui é um clássico problema de conservação do momento de energia. Esse princípio diz que em um sistema isolado, a energia inicial é igual a energia final.

Portanto se encontrarmos a energia desses instantes, podemos modelar o problema.

Por exemplo, inicialmente, a casca esférica, a polia e o bloco estão parados, logo o sistema possui apenas energia potencial.

E no fim, todos esses objetos estão em movimento e a energia potencial não existe mais.

Entendeu o esquema? Bora começar! 😉

Passo 2

Começando pela energia inicial, temos

U = m g h

Onde h é a altura 82 c m que o bloco cai.

E no instante final, o sistema possui apenas energia cinética.

Para a casca esférica a energia cinética é dada por

K e = I e ω e 2 2

Para a polia, a energia cinética é dada por

K p = I p ω p 2 2

E a energia cinética do bloco é

K b = m v 2 2

Somando todas as energias no instante final, temos que a energia final é dada por

K f = K e + K p + K b

K f = I e ω e 2 2 + I p ω p 2 2 + m v 2 2

Pelo princípio da conservação de energia, podemos dizer que U = K f

m g h = I e ω e 2 2 + I p ω p 2 2 + m v 2 2

Tranquilo até aqui? 👀

Passo 3

A velocidade tangencial da casca esférica, da polia e do bloco são as mesmas no instante final, então podemos dizer que

ω e = v R

ω p = v r

Substituindo no problema...

m g h = I e v R 2 2 + I p v r 2 2 + m v 2 2

m g h = I e v 2 2 R 2 + I p v 2 2 r 2 + m v 2 2

m g h = v 2 I e 2 R 2 + I p 2 r 2 + m 2

Não foi dado o momento de inércia da casca esférica, mas podemos obtê-lo como

I e = 2 M R 2 3

Logo

m g h = v 2 2 M R 2 3 2 R 2 + I p 2 r 2 + m 2

m g h = v 2 M 3 + I p 2 r 2 + m 2

Interessante, não é? 😎

Passo 4

Isolando v 2 em um lado da equação...

v 2 = m g h M 3 + I p 2 r 2 + m 2

Relembrando os dados dessa equação, temos m = 0,6 k g , g = 9,8 m / s 2 , h = 0,82 m , M = 4,5 k g , I p = 3,0 · 10 - 3 k g . m 2 , r = 0,05 m .

Substituindo em v 2

v 2 = 0,6 9,8 0,82 4,5 3 + 3 · 10 - 3 2 0,05 2 + 0,6 2 = 4,82 2,4 = 2

v = 2

v = 1,42 m / s

Fim! Iae, o que achou? Responde Aí! 😁

Resposta

v = 1,42 m / s

Exercícios de Livros Relacionados

O cume do monte Everest está 8850m acima do nível do mar. (a) Qual seria a energia gasta por um alpinista de 90k g para escalar o monte Everest a partir do nível do mar, se a única força que tivesse q
Uma bola de 50g é lançada de uma janela com uma velocidade inicial de 8,0m / s e com um ângulo de 30 ° acima da horizontal. Usando a lei de conservação da energia, determine (a) a energia cinética da
Uma bola de neve de 1,50k g é atirada para cima em um ângulo de 34,0 ° com a horizontal e com uma velocidade inicial de 20,0m / s . (a) Qual é a energia cinética da bola? (b) De quanto varia a energia
Uma locomotiva com uma potência de 1,5M W pode acelerar um trem de uma velocidade de 10m / s para 25m / s em 6,0m i n . (a) Calcule a massa do trem. Determine, em função do tempo (em segundos), (b) a
b) Qual é a rapidez da bola ao chegar no chão