Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade e Aceleração Médias no Movimento Circular

Ver Teoria
Exercício 4512345678910111213141516171819202122232425262728293031323334353637383940414243444647484950515253545556575859606162636465

Enunciado

UFSC, Sem Campus, Física 2, Listas de Física 1 - Profº Eduardo Duzzioni - Lista de Exercícios 1, Questão 11.

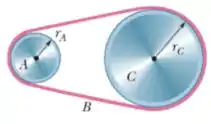
11) Na figura abaixo uma roda A de raio r A = 10   c m está acoplada por uma correia B a uma roda C de raio r B = 25   c m . A velocidade angular da roda A é aumentada a partir do repouso a uma taxa constante de 1,6   r a d / s 2 . Determine o tempo necessário para que a roda C atinja uma velocidade angular de 100   r e v / m i n , supondo que a correia não deslize.

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão temos duas rodas, a roda menor acelera a uma taxa de 1,6   r a d / s 2 e queremos saber qual é o tempo necessário para a roda maior atingir a velocidade de 100   r e v / m i n .

Tem ideia de como fazemos isso? 🤔

As rodas estão ligadas por uma correia, ou seja, a velocidade tangencial de ambas, são iguais, o mesmo podemos dizer para as acelerações tangenciais.

A aceleração tangencial de um movimento circular é dada por

a t = α r

Assim, se ambas as acelerações tangenciais são iguais, então

a t A = a t B

α A r A = α B r B

Tranquilo até aqui? 👀

Passo 2

Queremos saber a aceleração angular da roda B para descobrirmos o tempo do movimento.

Então isolando α B em um lado, temos

α B = α A r A r B

Se α A = 1,6   r a d / s 2 , r A = 0,1   m e r B = 0,25   m , substituindo na equação, temos

α B = 1,6 · 0,1 0,25

α B = 0,64   r a d / s 2

Por fim, se a aceleração é dada pelo variação de velocidade dividida pela variação do tempo, então

α B = ∆ ω B ∆ t

Isolando ∆ t

∆ t = ∆ ω B α B

A roda B sai do repouso até 100   r e v / m i n , convertendo isso para r a d / s , temos

100 r e v m i n · 2 π 60 = 10,47   r a d / s

Substituindo em ∆ t

∆ t = 10,47 0,64

∆ t = 16,36   s

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

∆ t = 16,36   s

Exercícios de Livros Relacionados

Pulsares são estrelas de nêutrons que emitem raios X e outras radiações de tal forma que nós, na Terra, recebemos pulsos de radiação dos pulsares em intervalos regulares iguais ao período de sua rotaç
Um próton sujeito a um campo magnético realiza um movimento helicoidal uniforme, com os seguintes parâmetros v x y = 5,00 x 10 5 m / s , a = 4,00 x 10 12 m / s 2 e v z = 2,00 x 10 4 m / s . Calcule o
As lâminas de um ventilador giram com velocidade angular dada por ω z t = γ - β t 2 , onde γ = 5r a d / s e β = 0,8r a d / s 3 . a) Calcule a aceleração angular em função do tempo. b) Calcule a aceler
Uma criança está empurrando um carrossel. O deslocamento angular do carrossel varia com o tempo de acordo com a relação θ t = γ t + β t 3 , onde γ = 0,4r a d / s e β = 0,012r a d / s 3 .a) Calcule a v
Uma roda gira em torno de um eixo que está na direção z . A velocidade angular ω z é - 6 rad/s para t = 0 , aumenta linearmente no decorrer do tempo e é + 8 rad/s para t = 7 s. Consideramos a rotação