UFSC, Sem Campus, Física 2, Listas de Física 1 - Profº Eduardo Duzzioni - Lista de Exercícios 1, Questão 16.
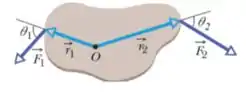
16) O corpo da figura abaixo pode girar em torno de um eixo perpendicular ao plano do papel passando por , e duas forças atuam sobre ele, como mostra a figura. Se , , , , e , qual é o torque resultante em relação ao eixo?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema queremos obter o torque resultante no objeto tendo duas forças atuando sobre ela.
A primeira força faz um ângulo com o eixo perpendicular ao eixo de rotação, é aplicado a uma distância e tem módulo .
A segunda força faz um ângulo com outro eixo perpendicular ao eixo de rotação, é aplicado a uma distância e tem módulo .
Como podemos obter o torque resultante? 🤔
O torque é a força de rotação de um objeto, então apenas as componentes paralelas a e geram torques.
Podemos começar desenhando o diagrama de forças do sistema para obter as componentes de e que geram torque.
Bora lá! 😊
Passo 2
Desenhando o sistema, temos
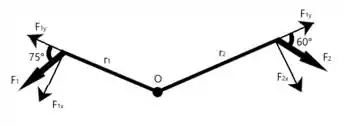
Perceba que as componentes e são as forças que geram torque, logo pela regra dos senos, temos
O torque nada mais é que a força perpendicular a multiplicado pela distância onde a força é aplicada.
Ou simplesmente podemos dizer que o torque é o produto vetorial de e .
Considerando o sentido horário como o sentido positivo, temos que o torque resultante será
Perceba que é negativo pois faz o objeto girar no sentido oposto.
Substituindo os dados do enunciado, temos
Fim! Iae, o que achou? Responde Aí! 😁
