UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 17
Use o gráfico da função para desenhar o gráfico das funções abaixo.
a)
b)
c)
d)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função conhecida e pediu pra gente obter o gráfico de outras funções a partir dela.
Repare que nós temos constantes sendo adicionadas, multiplicadas ou subtraídas dentro ou fora do argumento da função. Quando isso acontece, existem algumas propriedades que nos ajudam a reconhecer quando o gráfico é expandido, contraído ou deslocado. Olha só:
Então, vamos identificar onde temos deslocamentos horizontais e verticais e onde temos reflexões e expansões no gráfico da função para esboçar esse gráfico a partir de .
Vamos lá!
Passo 2
Na letra a), temos . Nós sabemos que representa o gráfico de uma parábola com concavidade voltada para cima (porque o coeficiente de é positivo), centrada na origem, ou seja:
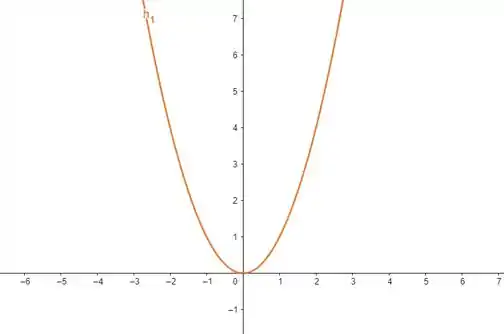
Para , nós adicionamos na função, então nós deslocamos em unidade para cima. Nosso gráfico fica assim:
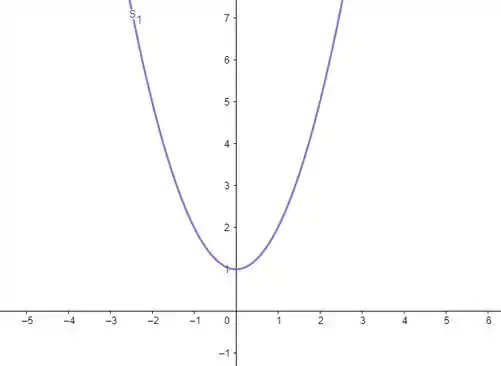
Passo 3
Na letra b), temos . Repare que nós estamos subtraindo do argumento da função. Olhando lá na tabelinha do passo , isso representa um deslocamento em unidade para direita do gráfico de . Então, o gráfico de será:
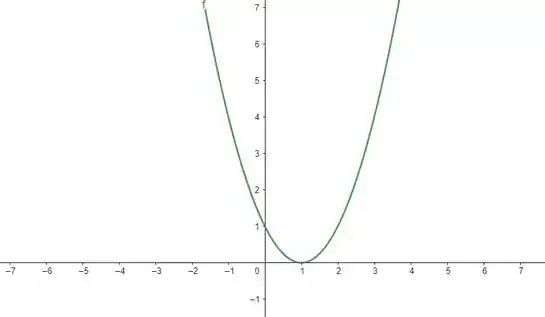
Passo 4
Na letra c), temos . Repare que a gente tá multiplicando a função toda por , então temos . Olhando lá no passo e sabendo que , nós vemos que precisamos refletir o gráfico de em torno do eixo . Então, temos:
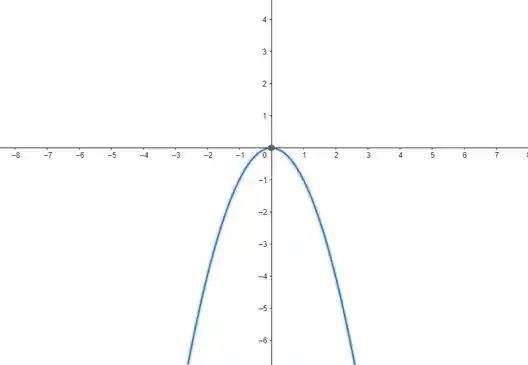
Passo 5
Na letra d), temos . Agora nós estamos subtraindo do argumento da função e subtraindo da função inteira. Ou seja, nós temos e . Sabendo que e olhando as relações do passo , a gente percebe que para obter o gráfico de precisamos deslocar o gráfico de em unidade para direita e deslocar o gráfico de em unidades para baixo. Então, encontramos o gráfico de :
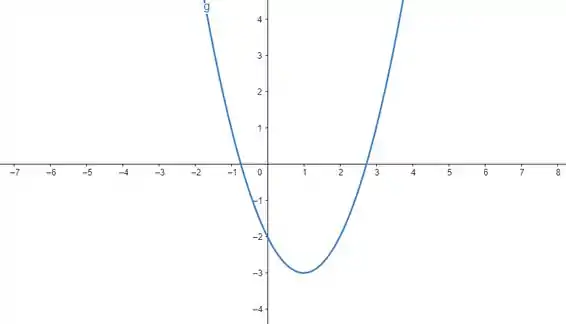
Prontinho, galera! Até a próxima! 😉