UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 3
Seja uma função com domínio simétrico em relação à origem (por exemplo, um domínio da forma ). Dizemos que é uma função par se para todos . Se para todos , dizemos que é uma função ímpar. Por exemplo, é uma função par, pois para todo , . A função é uma função ímpar, pois para todo , . A função não é nem par nem ímpar, pois e essa expressão não é igual a para todo . O gráfico das funções pares possui a propriedade de ser simétrico em relação ao eixo das ordenadas (isto é, a metade esquerda e a metade direita do gráfico são espelhadas). O gráfico das funções ímpares possui a propriedade de ser simétrico em relação à origem (isto é, se o ponto pertence ao gráfico , então o ponto também pertence). Complete o gráfico da função em que uma parte do gráfico está desenhada abaixo, sabendo que:
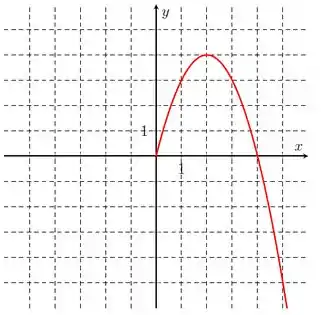
a) A função é par
b) A função é ímpar
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu o gráfico incompleto de uma função e pediu pra gente completar supondo que essa função seja par e depois supondo que essa função seja ímpar.
Como o gráfico das funções pares possui a propriedade de ser simétrico em relação ao eixo das ordenadas, para completar o gráfico sabendo que é uma função par, basta refletir a parte dada em relação ao eixo . E sabendo que o gráfico das funções ímpares possui a propriedade de ser simétrico em relação à origem, para completar o gráfico sabendo que é uma função ímpar, basta refletir a parte dada em relação à origem.
Vamos lá!
Passo 2
Galera, vamos completar o gráfico da função sabendo que ela par espelhando a parte dada em relação ao eixo . Fica assim:
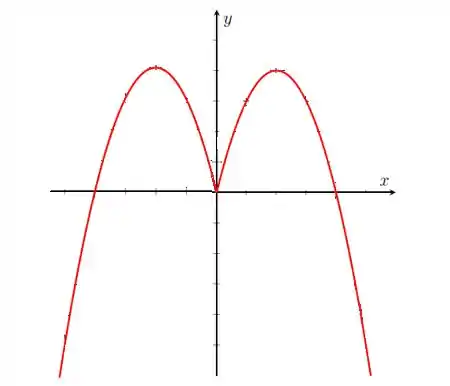
Passo 3
Na letra b), sabendo que a função é ímpar, vamos espelhar o gráfico em relação à origem e temos:
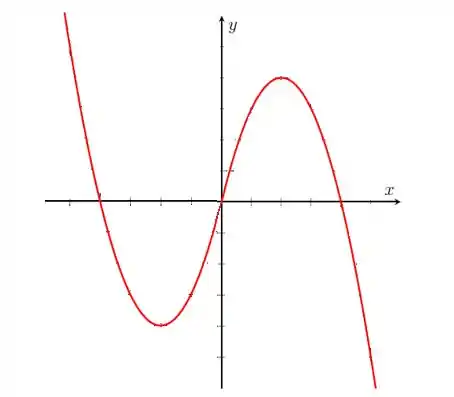
Repare que para refletir em relação à origem a gente faz uma reflexão no eixo seguida de uma reflexão no eixo , beleza?
Prontinho, galera! Até a próxima! 😉