UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 19jk
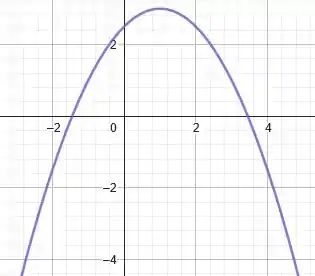
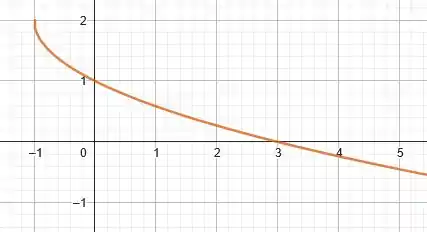
Faça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
Passo 1
Olá, tudo bem com vocês?
O enunciado dessa questão é bem direto, nos foram dadas algumas funções e precisamos desenhar os seus gráficos. Mas, para fazer isso vamos compará-las com outras funções mais simples cujos gráficos são conhecidos.
A partir disso, iremos analisar qual o efeito produzido no gráfico da nossa função de interesse. Ou seja, se foi uma reflexão em torno de um eixo, uma translação, ou algo do tipo.
Sacaram a ideia?
Então vamo nessa!
Passo 2
Começando pelo nosso item , temos a função:
Bom, primeiro precisamos identificar a nossa função mais básica envolvida em . Como temos um termo dependente de elevado ao quadrado, podemos fizer que a função mais básica é:
Cujo gráfico é o seguinte:
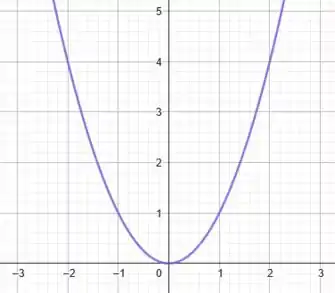
Em comparação a , a diferença é que subtraímos uma unidade em , multiplicamos a função resultante por , depois dividimos tudo por e no fim ainda somamos unidades à função como um todo.
Vamos destrinchar com calma o efeito de cada uma dessas ações no gráfico de , beleza?
Pra começar, quando subtraímos uma unidade em deslocamos a nossa curva de horizontalmente. Agora, para um valor de ser equivalente ao valor da função em , precisamos que seja uma unidade maior do que . Ou seja, o efeito provocado na prática é transladar toda a função para a direita em uma unidade. Assim:
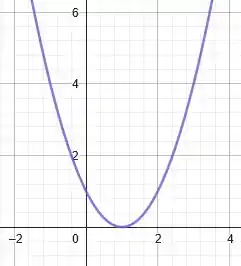
Massa! A próxima ação foi multiplicar a função por . Quando fazemos isso, invertemos todos os valores das ordenadas dos pontos da curva. Ou seja, na prática nós refletimos a curva em relação ao eixo .
Após isso, ainda dividimos a função resultante por . Isso significa que estamos achatando a função, pois diminuímos cada ordenada pela metade. Assim, temos a seguinte curva:
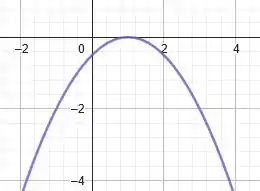
Por fim, somamos à todos os pontos da função unidades. Isso é equivalente a transladar a função unidades para cima. Portanto, finalizando, teremos que o gráfico de é:
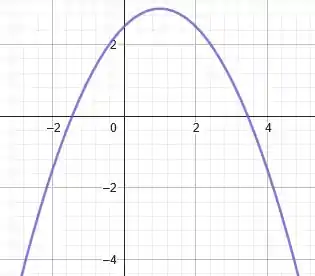
Prontinho!
Passo 3
Vamos agora para o item . Aqui temos a função:
O raciocínio é bem parecido com o item anterior. A nossa função mais básica envolvida em é:
Chegamos em a partir de somando uma unidade em , depois multiplicamos a função por e por fim somamos duas unidades à função como um todo.
Como comentamos anteriormente, ao somarmos uma unidade em , estamos transladando a função uma unidade para a esquerda. Assim, ficamos com o seguinte gráfico parcial:
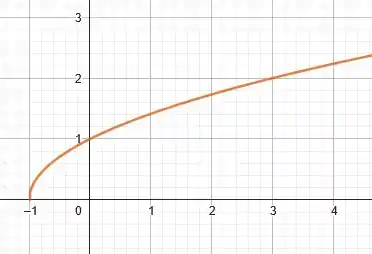
Ao multiplicar a função por iremos refletir a sua curva em relação ao eixo .
Teremos:
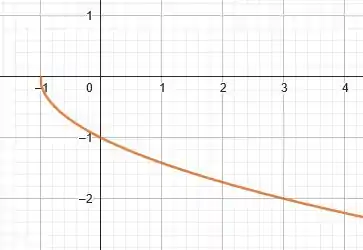
Por fim, ao somarmos duas unidades na função como um todo, estamos transladando a curva verticalmente para cima em duas unidades. Logo, finalizando, teremos o seguinte gráfico para a função :
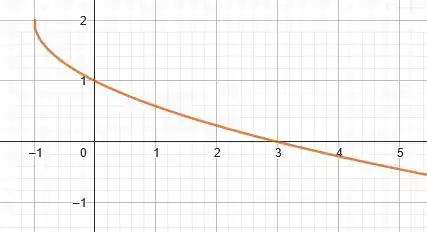
Prontinhooo!
Com isso matamos mais uma questão 😊
Obrigado pela atenção gente!!
Resposta
