UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 10
Nos itens abaixo, faça o gráfico da inversa da função cujo gráfico está representado.
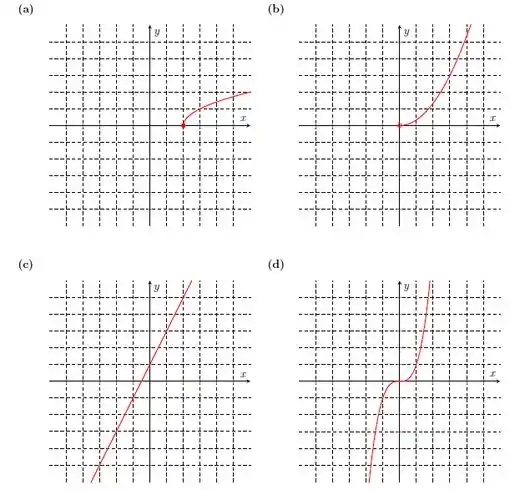
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu alguns gráficos de funções e pediu pra gente fazer o gráfico das inversas dessas funções.
Nós vamos precisar lembrar que os gráficos cartesianos de e de são simétricos em relação à bissetriz do primeiro e terceiro quadrantes do plano cartesiano. A bissetriz é a reta que divide os dois eixos a partir do vértice. Então, basta a gente refletir o gráfico de em torno dessa reta para obter o gráfico de .
Vamos lá!
Passo 2
Na letra a), nós temos o gráfico:
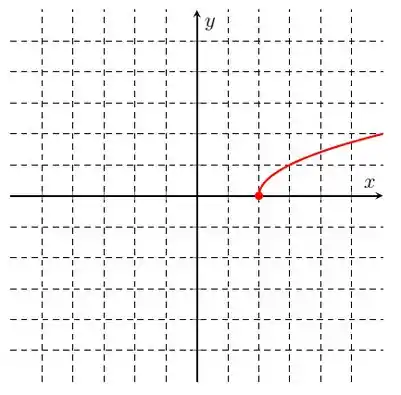
Traçando a bissetriz e refletindo essa curva em todo dela, temos o gráfico da função inversa:
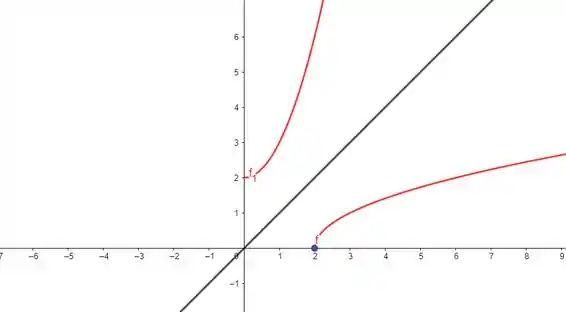
Passo 3
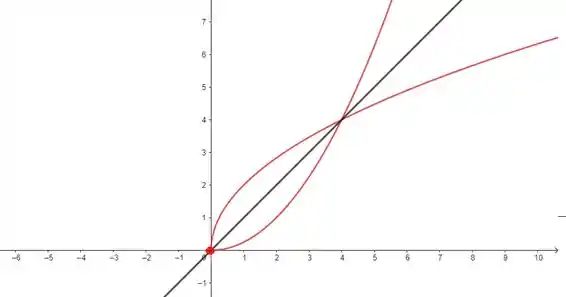
Na letra b), temos o gráfico:
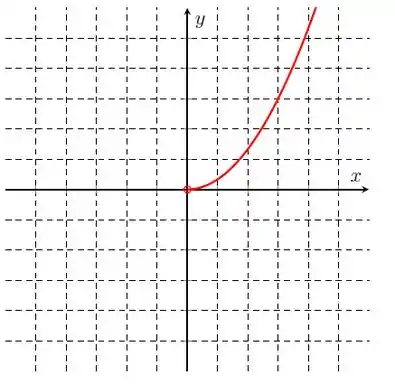
Traçando a bissetriz e refletindo essa curva em todo dela, temos o gráfico da função inversa:
Passo 4
Na letra c), temos o gráfico:
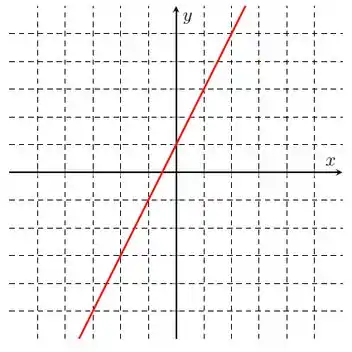
Traçando a bissetriz e refletindo essa curva em todo dela, temos o gráfico da função inversa:
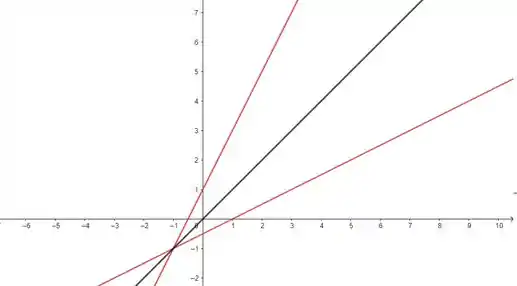
Passo 5
Na letra d), temos o gráfico:
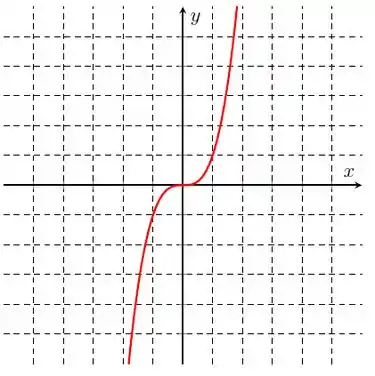
Traçando a bissetriz e refletindo essa curva em todo dela, temos o gráfico da função inversa:
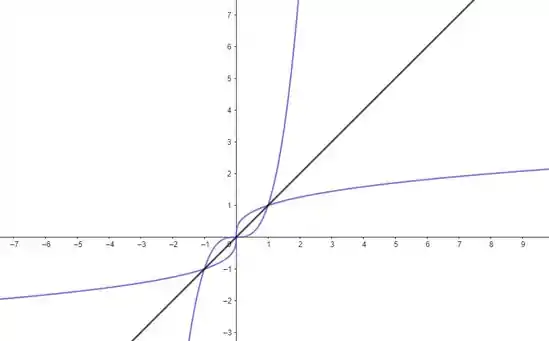
Prontinho, galera! Até a próxima! 😉