UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 19abc
Faça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
.
.
Passo 1
Fala aí pessoal, tudo beleza?
O enunciado dessa questão é bem direto, nos foram dadas algumas funções e precisamos desenhar os seus gráficos. Mas, para fazer isso vamos compará-las com outras funções mais simples cujos gráficos são conhecidos.
A partir disso, iremos analisar qual o efeito produzido no gráfico da nossa função de interesse. Ou seja, se foi uma reflexão em torno de um eixo, uma translação, ou algo do tipo.
Sacaram a ideia?
Então vamo nessa!
Passo 2
Começando pelo item , temos a função:
A função mais básica que está envolvida em é:
É a nossa querida parábola! O seu gráfico é uma parábola virada pra cima, com mínimo em e simétrica em relação ao eixo .
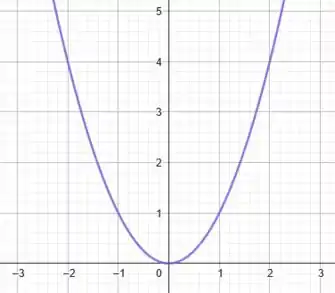
Comparando com vemos que a grande diferença é que em subtraímos uma unidade.
Qual será o efeito dessa subtração?
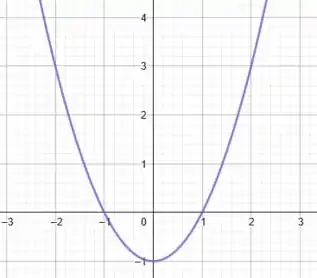
Pensa comigo, pra cada ponto da parábola original, estaremos subtraindo uma unidade. Assim, os novos pontos passarão a ser . Ou seja, na prática, é como se estivéssemos deslocando a curva para baixo em uma unidade.
Assim, o gráfico passa a ser:
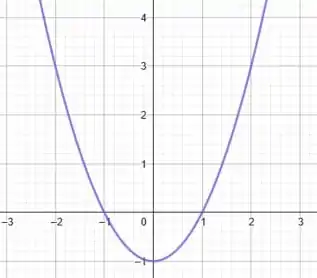
Perfeito!
Passo 3
No item , temos a função:
Aqui, o nosso gráfico base será:
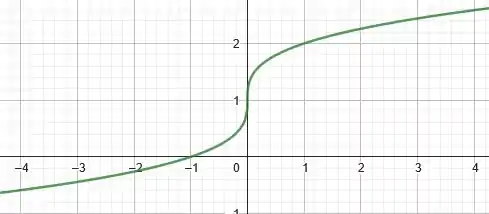
Bora dar uma revisada na forma do gráfico dessa função:
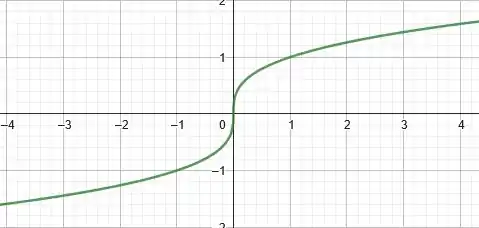
A grande diferença comparando com é que estamos somando uma unidade. Ou seja, usando o mesmo raciocínio do passo anterior, é como se estivéssemos deslocando a curva uma unidade para cima.
Assim, transladando o gráfico de uma unidade para cima, temos:
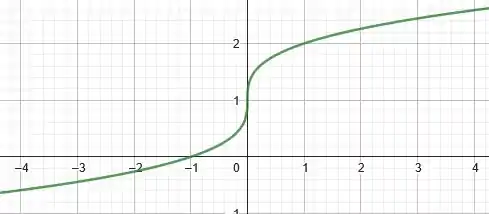
Muito bom!
Passo 4
Por fim, vamos analisar a função do item :
Aqui é um pouquinho mais difícil enxergar a função básica que está envolvida. Mas, se chamarmos
Vemos que se trata de:
Ou seja, lá no fundo é uma parábola. A diferença é que subtraímos unidades em .
O que será que isso vai acarretar na nossa função?
Bom agora temos:
Isso significa que na nossa nova função, só teremos a “equivalência” entre a parábola e quando pegarmos valores de unidades maiores. Por exemplo:
Entenderam?
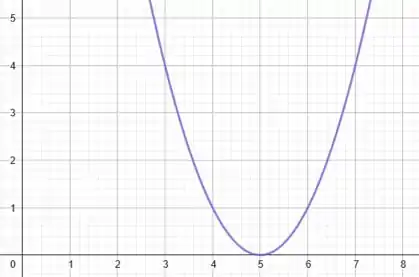
Ou seja, na prática estamos transladando toda a nossa curva para a direita em unidades. Assim, nosso gráfico vai ficar:
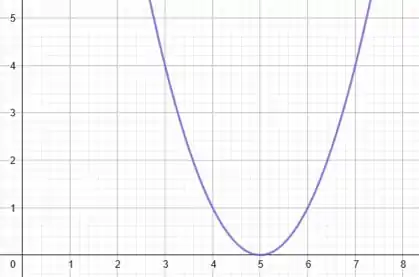
Prontinho!!! Entenderam bem pessoal?
Obrigado pela atenção 😊
Resposta
