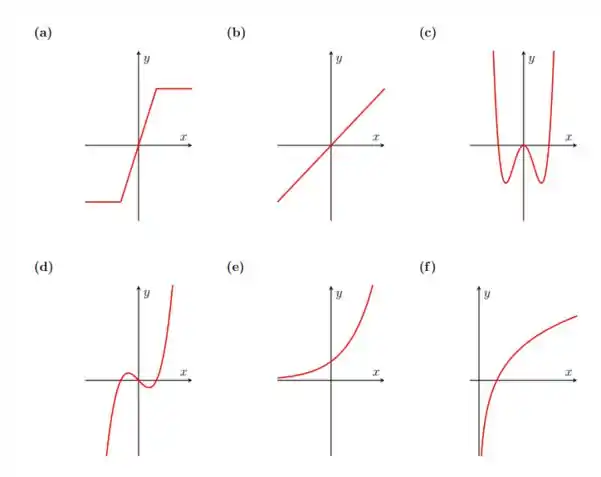
Diga quais das funções abaixo são injetoras, sobrejetoras ou bijetoras, considerando ℝ como contra-domínio para todas elas.
Passo 1
Oiie, tudo bem?
O enunciado pede para analisarmos se as funções que tem os seguintes gráficos
são injetoras, sobrejetoras ou bijetoras, tomando como contradomínio todos os reais. Mas o que são estas coisas? Uma função injetora é aquela que para todo valor de você obtém um único valor de exclusivo para a sua escolha de . Uma função é sobrejetora se o subconjunto imagem, for igual ao conjunto contradomínio, isso depende da nossa escolha, aqui iremos usar o contradomínio como os reais. A função bijetora é tanto injetora quanto bijetora! Vamos tentar analisar isso um a um! Saca só!
Passo 2
Para a função que tem gráfico
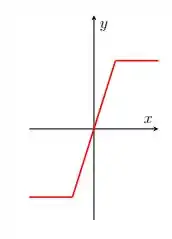
podemos dizer que ela não é injetora, sequer é sobrejetora. Note que a imagem (ou o gráfico) vai até um valor máximo e mínimo de onde se torna constante, portanto, com certeza o subconjunto imagem é menor que o contradomínio que toma todo o eixo . Note também que quando o gráfico se torna horizontal, todo valor de irá levar ao mesmo valor de , portanto, existem diversos que levam ao mesmo . Essa função não é injetora, nem sobrejetora, e portanto, não é bijetora! Vamos para a próxima agora!
Passo 3
Para que tem gráfico
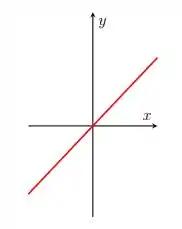
Note que todo valor de resulta em um valor diferente para , portanto, a função é injetora! Ela também é sobrejetora, note que os valores possíveis de vão do topo do eixo vertical até a base do eixo vertical , sem pular nenhum valor, portanto, o subconjunto imagem é igual ao contradomínio. Se ela é tanto injetora quanto sobrejetora, ela é bijetora! Vamos para a próxima!
Passo 4
Para que tem gráfico
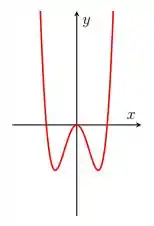
Novamente, esta função não é injetora, nem é sobrejetora. Ela não pode ser injetora pois é uma função que é simétrica em relação ao eixo , desta forma, valores simétricos de levam ao mesmo valor de (Adiciono aqui que nenhuma função “par” pode ser injetora!!!). Ela não é sobrejetora pois tem um mínimo no eixo , ou seja, existe todo um grupo de valores reais que não pertencem a imagem! Se ela não é injetora, nem sobrejetora, não pode ser bijetora! Mais um!
Passo 5
Para que tem gráfico
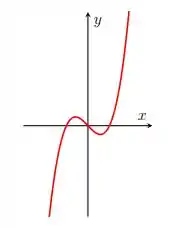
Essa função não é injetora, mas ela é sobrejetora! Uma maneira de notar se uma função é injetora é ver se é possível traçar uma linha horizontal que cruze o gráfico mais de uma vez, se for possível, ela não é injetora, note que é possível traçar uma horizontal que cruza o gráfico em três pontos, portanto, existem ao menos três valores de que resultam no mesmo . No entanto, ela é sobrejetora, note que o gráfico vai de até no eixo sem pular nenhum valor, portanto, a imagem é igual aos reais, que é nosso contradomínio! A função não é injetora, portanto, não é bijetora! Faltam apenas dois agora! Vamos lá!
Passo 6
Para que tem gráfico
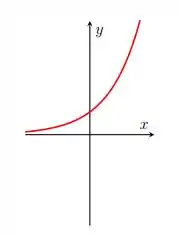
Esta função é injetora, mas não é sobrejetora! Note que todo valor de está relacionado a apenas um resultado no eixo ! Mas a função não é sobrejetora, toda a parte abaixo do eixo não faz parte da imagem, e faz parte do contradomínio, que é os reais! Se a função não é sobrejetora, também não pode ser bijetora! Falta apenas mais uma! Vamo que vamo!
Passo 7
Para que tem gráfico
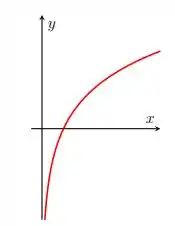
Essa função é injetora e sobrejetora! Note que todo pertencente ao domínio da função leva a um diferente, portanto, a função é injetora! Ela também é sobrejetora já que o gráfico vai de no eixo até , portanto, a imagem é igual aos reais! Se a função é injetora e sobrejetora, ela é bijetora! Uff… Foram todas! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Não é Injetora nem sobrejetora portanto não é bijetora.
É injetora e sobrejetora portanto é bijetora.
Não é injetora nem sobrejetora portanto não é bijetora.
Não é injetora, mas é sobrejetora, não é bijetora.
É injetora, mas não é sobrejetora, não é bijetora.
É injetora e sobrejetora, portanto, é bijetora.