Sejam uma função e um intervalo contido no domínio de . Dizemos que é crescente em se para quaisquer e com . Em outras palavras, o valor de aumenta à medida que aumenta. Similarmente dizemos que é decrescente em se para quaisquer e com . Quando dizemos que é crescente (sem mencionar intervalo), significa que é crescente em todo seu domínio (o mesmo se aplica para decrescente). Por exemplo, considere a função cujo gráfico é dado pela figura abaixo.
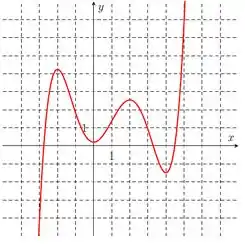
Note que a função é crescente em , em e em e é decrescente em e em . Nos itens abaixo, diga os intervalos de crescimento e decrescimento das funções.
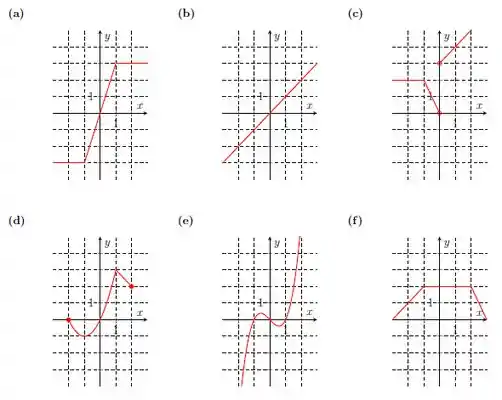
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu alguns gráficos de funções e pediu pra gente determinar os intervalos de crescimento e decrescimento das funções.
Para isso, vamos olhar os intervalos onde o valor de aumenta à medida que aumenta (crescimento) e os intervalos onde o valor de diminui à medida que aumenta (decrescimento).
Vamos lá!
Passo 2
Galera, olhando o gráfico da letra a), temos:
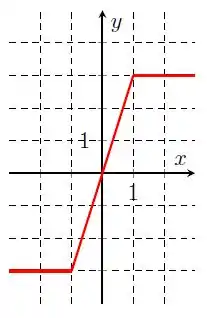
Repare que de a , a função se mantém constante. Depois ela passa a crescer de a e volta a ser constante de a . Assim, temos:
Passo 3
Na letra b), temos:
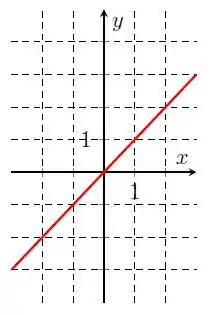
Repare que temos uma reta que cresce infinitamente, então podemos dizer que a função é crescente em todo seu domínio, ou seja:
Passo 4
Na letra c), temos:
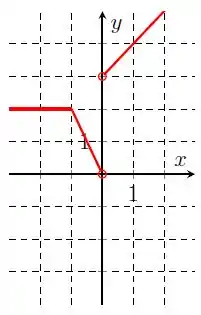
Temos uma função que é constante de até . Em seguida, ela decresce até (onde ela não está definida, repare na bolinha aberta) e depois a função cresce de até . Logo,
Passo 5
Na letra d), temos:
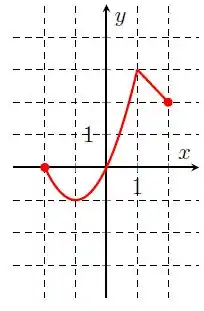
Nossa função decresce de até . Depois a curva passa a crescer de até , e volta a decrescer de até . Assim, temos:
Passo 6
Na letra e), temos:
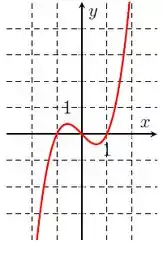
Repara que nossa curva cresce de até . Depois decresce de até , e volta a crescer de até .
Passo 7
Na letra f), temos:
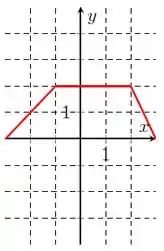
Repara que nossa função cresce de até , depois ela se mantém constante de a , e passa a decrescer de até . Logo,
Prontinho, galera! Até a próxima! 😉
Resposta
a)
b)
c) e
d) e
e) e
f) e