UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 14
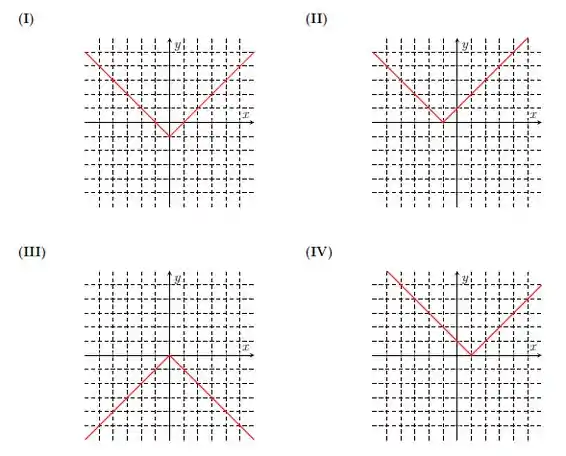
Associe as funções aos gráficos.
a)
b)
c)
d)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu algumas funções modulares e pediu pra gente encontrar o gráfico delas entre os gráficos dados.
Pra isso, a gente precisa lembrar que o gráfico da função modular é a reunião de duas semirretas de origem , que são as bissetrizes do e do quadrantes. Vamos nos basear nisso e ir deslocando essas retas a depender da regra de formação da função.
Vamos lá!
Passo 2
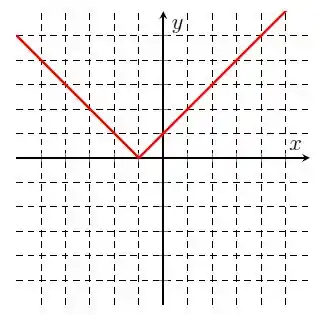
Na letra a), temos :
Como a função modular é definida por:
Então, temos a reta no primeiro quadrante e a reta no segundo quadrante. Nós podemos ver isso no gráfico :
Passo 3
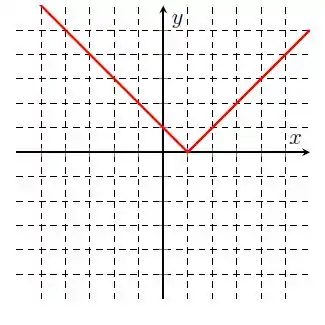
Na letra b), temos .
Então, temos a reta no primeiro quadrante e a reta no segundo quadrante. Nós podemos ver isso no gráfico :
Passo 4
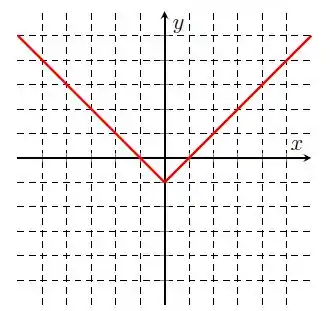
Na letra c), temos . Nosso gráfico tem a forma do gráfico de , mas deslocado de unidade para baixo. Isso acontece no gráfico :
Passo 5
Na letra d), temos . Nossa função tem a forma do , mas virado para baixo, por causa do sinal negativo. Então, temos o gráfico :
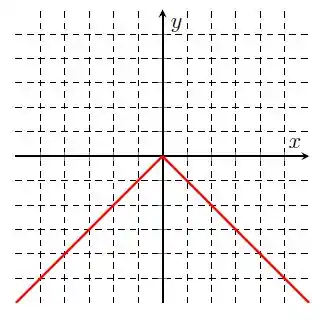
Prontinho, galera! Até a próxima! 😉