UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 19ghi
Faça o gráfico das funções abaixo relacionando o gráfico procurado com um gráfico já conhecido.
.
.
Passo 1
Fala aí pessoal, tudo certinho?
O enunciado dessa questão é bem direto, nos foram dadas algumas funções e precisamos desenhar os seus gráficos. Mas, para fazer isso vamos compará-las com outras funções mais simples cujos gráficos são conhecidos.
A partir disso, iremos analisar qual o efeito produzido no gráfico da nossa função de interesse. Ou seja, se foi uma reflexão em torno de um eixo, uma translação, ou algo do tipo.
Sacaram a ideia?
Então vamo nessa!
Passo 2
Começando pelo item , temos a função:
Vamos começar identificando a função base:
É bem importante perceber que essa função só tem domínio nos valores não-negativos de . Podemos até relembrar o formato do seu gráfico:
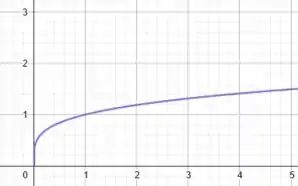
A grande mudança de em relação a é que multiplicamos, dentro da raiz, por .
Como a nossa função só existe para valores não-negativos dentro da raiz, o que vai ocorrer é uma “inversão do domínio”. Antes, o domínio de era os números reais não-negativos, agora que multiplicamos por o domínio de será dado pelos números reais não-positivos.
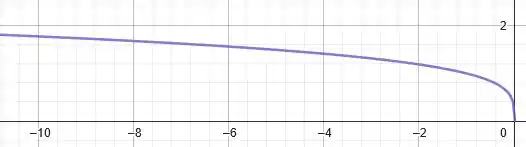
Na prática é como refletirmos a curva em relação ao eixo .
Assim, vamos o seguinte gráfico para :
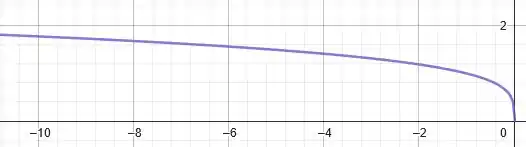
Tudo tranquilo até aqui?
Passo 3
No item , temos a função:
O raciocínio é bem semelhante ao item anterior, a diferença é que a nossa função base:
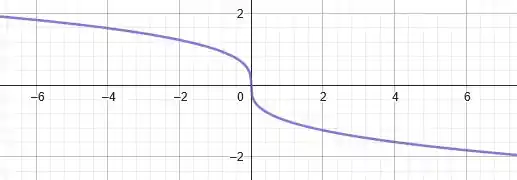
possui domínio em todos os reais. O formato do seu gráfico é o seguinte:
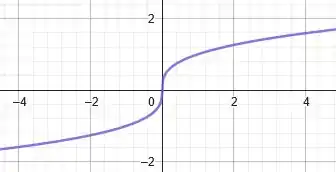
Porém, como multiplicamos o por , o efeito provocado no gráfico continua sendo o mesmo. Iremos refletir essa curva em relação ao eixo . Assim, vamos ter para o seguinte gráfico:
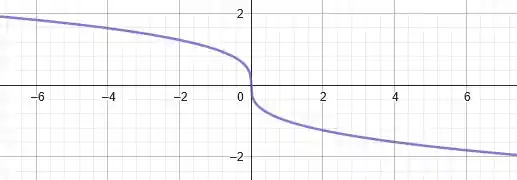
Muito bom!
Passo 4
Pra finalizar, no item temos a função:
A função mais básica envolvida em é:
Que possui o gráfico:
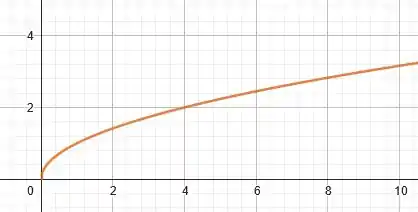
Comparando e vemos que em somamos unidades em e depois subtraímos a função como um todo em unidades.
Quando somamos unidades em , estamos deslocando o gráfico de para a esquerda, pois agora teremos a equivalência entre e para valores de quatro unidades menores do que . Se liga nesse exemplo:
Massa! Já quando subtraímos a função como um todo, estamos transladando a curva verticalmente para baixo.
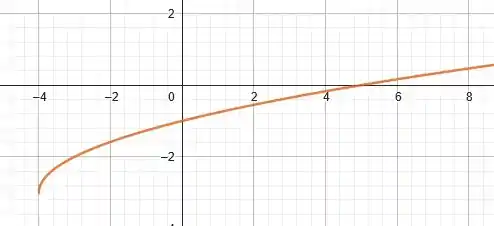
Assim, iremos transladar a curva em quatro unidades para a esquerda e três unidades para baixo. Ficamos com o seguinte gráfico:
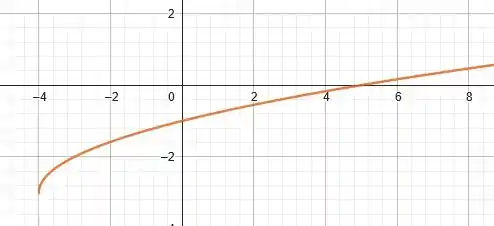
Prontinho pessoal! Obrigado pela atenção e até a próxima 😊
Resposta
