UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 21ab
Nos itens abaixo, o gráfico da função está em vermelho e o da função em azul. Encontre a regra de formação de a partir de .
Passo 1
Fala aí galera, tudo bom?
Nessa questão precisamos determinar a lei de formação de sabendo apenas a lei de formação de uma função , e conhecendo os gráficos de e .
A grande ideia aqui é entender quais operações foram realizadas no gráfico de (reflexão, translação, esticamento) e como essas operações alteram a lei de formação de . Sabendo disso devemos chegar na lei de formação de .
Para seguir esse caminho é importante lembrarmos como as alterações no gráfico se manifestam matematicamente, vamo dar uma revisada:
- Se transladamos o gráfico de uma função em unidades pra cima, é porque matematicamente fizemos:
- Se transladamos o gráfico de uma função em unidades pra baixo, é porque matematicamente fizemos:
- Se transladamos o gráfico de uma função em unidades pra esquerda, é porque matematicamente fizemos:
- Se transladamos o gráfico de uma função em unidades pra direita, é porque matematicamente fizemos:
- Se refletimos o gráfico de uma função em relação ao eixo , é porque matematicamente fizemos:
- Se refletimos o gráfico de uma função em relação ao eixo , é porque matematicamente fizemos:
Massa! Vamos agora analisar cada item individualmente 😊
Passo 2
Começando pelo item , temos a função:
E, nos foi dada a seguinte relação entre os gráficos:
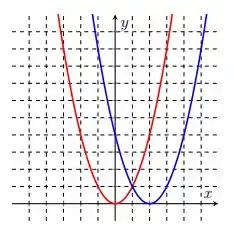
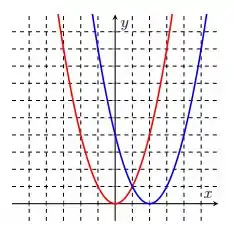
Lembrando que o gráfico de está em vermelho. Assim, podemos ver que o gráfico em azul é uma simples translação da curva vermelha para a direita em duas unidades.
Logo, como vimos que a translação para a direita é equivalente a fazer:
Teremos, para as duas unidades transladadas:
Perfeito!
Passo 3
Indo agora para o item temos a função dada por:
Bora dar uma olhadinha no seu gráfico:
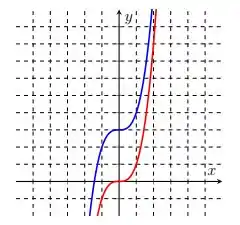
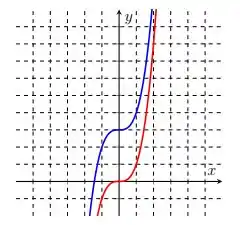
Comparando o gráfico de ( em vermelho) e o de (em azul), vemos que o gráfico em azul está transladado duas unidades para cima. Uma dica pra perceber isso é olhar onde temos . Assim, já que foi transladada unidades para cima, temos:
Prontinho! Matamos mais uma gente 😊