UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 18cd
Use o gráfico da função para desenhar o gráfico das funções abaixo.
.
.
Passo 1
Eaí gente, tudo tranquilo?
Nessa questão precisamos desenhar o gráfico de duas funções:
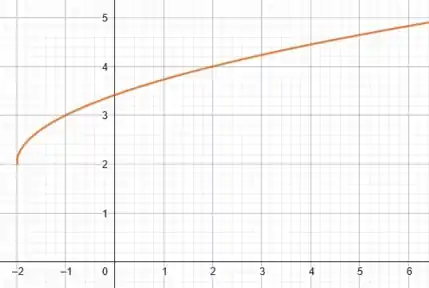
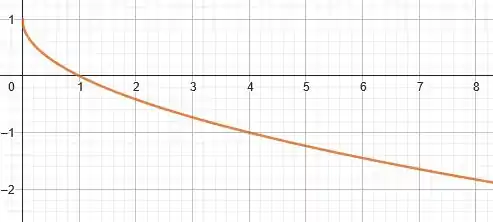
Mas para fazer isso podemos partir do gráfico da função . Vamo dar uma revisada na carinha dele:
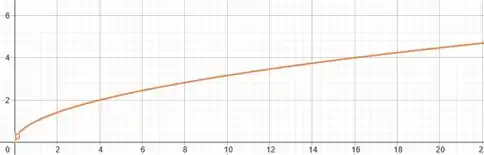
Ele só é válido para o eixo positivo dos .
Assim, nosso objetivo será analisar com as mudanças em influenciam no gráfico de , ou seja, se iremos transladar o gráfico pra cima, pra baixo, direita ou esquerda. Beleza?
Vamo nessa!
Passo 2
Começando por
Temos duas mudanças em relação a . Primeiramente onde tem o foram acrescentadas duas unidades, e à função como um todo também foram somadas duas unidades. É como se tivéssemos:
onde
Então, analisando o efeito dessa mudança de por , vemos que para a curva de coincidir com a curva de , precisamos subtrair duas unidades em . Por exemplo:
Ou seja, na prática estamos deslocando toda a curva para a esquerda em duas unidades.
Mas, além disso também somamos à função duas unidades. Isso faz com que os pontos sejam transladados duas unidades para cima, se tornando .
Fazendo essas duas translações na nossa curva de , temos:
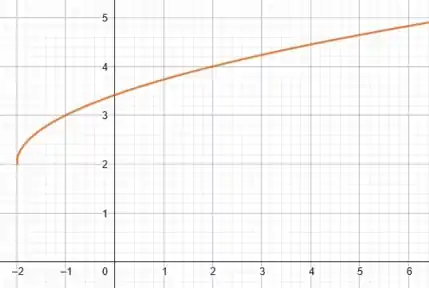
Boaaa! Essa parte já foi!
Passo 3
A próxima função é
Aqui, comparando com , também notamos duas mudanças: multiplicamos primeiro por e depois somamos uma unidade à função como um todo. Ou seja:
Vamos analisar cada uma dessas mudanças!
Quando multiplicamos por , para cada pontinho estamos pegando em o seu simétrico no eixo . Ou seja, estão se tornando .
Isso é equivalente a refletir a curva em relação ao eixo , beleza?
Já quando somamos uma unidade à função como um todo, estamos aumentando os seus valores no eixo em uma unidade, ou seja, estamos transladando a função para cima. Assim, vamos ter:
Conseguiram sacar a ideia das translações e reflexões nessa questão?
É isso pessoal, obrigado pela atenção! Até a próxima 😊
Resposta
