UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 18ab
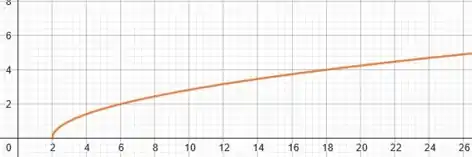
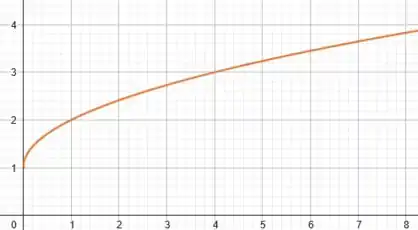
Use o gráfico da função para desenhar o gráfico das funções abaixo.
.
.
Passo 1
Eaí pessoal, como vocês estão?
Nessa questão precisamos desenhar o gráfico de duas funções:
Mas para fazer isso podemos partir do gráfico da função . Vamo dar uma revisada na carinha dele:
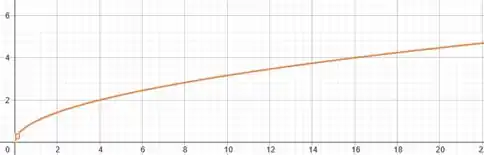
Ele só é válido para o eixo positivo dos .
Assim, nosso objetivo será analisar com as mudanças em influenciam no gráfico de , ou seja, se iremos transladar o gráfico pra cima, pra baixo, direita, ou esquerda. Beleza?
Vamo nessa!
Passo 2
Começando pelo item , precisamos desenhar o gráfico da função:
Comparando com a nossa função , podemos dizer que:
onde:
Isso significa que o gráfico de só coincide com a curva de quando está duas unidades maior. Ou seja, quando a curva está deslocada para a direita. Assim, basta pegarmos a curva e transladá-la duas unidades para a direita (ou ainda deslocar o eixo duas unidades para a esquerda). Vamos ter que:
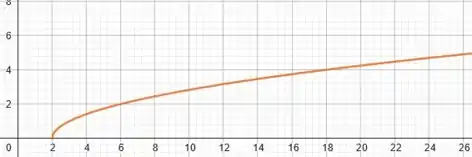
Muito bom!!
Passo 3
Vamos analisar agora o item , temos a função:
Então, comparando com a única diferença é que somamos uma unidade à função. Ou seja:
Assim, é como se cada ponto fosse agora acrescido de uma unidade em , se tornando . Ou seja gente, na prática, estamos trasladando toda a curva para cima em uma unidade. Sacaram?
Assim, vamos ter:
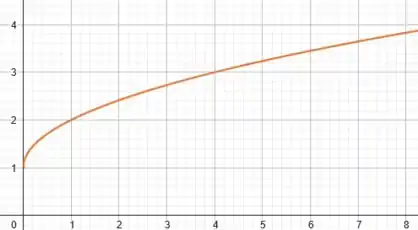
Prontinhooo!! Conseguiram entender bem o raciocínio?
Responde Aí!
Resposta
